---

П. Г. Кузнецов

Искусственный интеллект и разум человеческой популяции

Эвристическое программирование, эвристические решения, машинное распознавание образов, машинное моделирование интеллектуальной деятельности, программа общего решателя проблем, общая теория систем и многие другие научные направления различными путями идут к решению одной и той же задачи. Эта задача возникает там, где человек, серьезно занятый наукой, приходит к мысли, что его познания составляют ничтожную часть того, что ему хотелось бы знать. В этой ситуации, сознание ограниченности собственного интеллекта (связанной с такими естественными факторами, как время жизни и чисто физические возможности индивидуума) приводит к пониманию необходимости ее преодоления.

Наиболее ярко и точно эту проблему довольно давно представил У. Р. Эшби в своей замечательной работе: “Схема усилителя умственных способностей”. Эшби отмечает [1], что: “...инженеры средних веков, знакомые с принципом рычага, зубчатого колеса и блока, должно быть, часто говорили, что поскольку никакая машина, приводимая в действие человеком, не может дать больше работы, чем он в нее вкладывает, то никакая машина не может усиливать мощность человека. Но теперь мы видим, как один человек заставляет вращаться все колеса на заводе, бросая уголь в топку. Поучительно разобрать, как именно современный кочегар опровергает догмат средневекового инженера, все же оставаясь подчиненным закону сохранения энергии.

Небольшое размышление показывает, что этот процесс имеет две стадии. В первой стадии кочегар поднимает уголь в топку; в этой стадии энергия строго сохраняется. Попадание угля в топку представляет начало второй стадии, в которой энергия тоже сохраняется, по мере того как сжигание угля приводит к производству пара и, наконец, к вращению колес на заводе. Заставив весь процесс протекать двумя стадиями, связанными с двумя порциями энергии, величины которых могут меняться до некоторой степени независимо, современный инженер может получить общее усиление мощности”.

Далее Эшби ставит вопрос о том, что подобного рода проблема имеет место и для усилителя умственных способностей.

Нам хотелось бы несколько изменить точку зрения на эту же самую проблему. Мы будем рассматривать не разум отдельного индивидуума, а разум всей человеческой популяции. Можно возразить, что разумом обладают только отдельные индивидуумы, а не человеческая популяция в целом. Конечно, в настоящее время человеческая популяция еще не обладает коллективным разумом, но она обладает “коллективной памятью”. Эта “коллективная память” сосредоточена преимущественно в книгах и творениях человеческих рук. “Коллективная память” наших библиотек является потенциальной памятью – она оживает тогда и только тогда, когда живой индивидуум активно владеет этим богатством. Теперь мы можем уточнить нашу точку зрения – можно ли “потенциальную коллективную память” наших библиотек превратить в “оперативную память” человеческой популяции?

Высказывая сугубо личную точку зрения, я хотел бы думать, что это не только возможно, но и исторически необходимо. Человечество в настоящий момент переживает эпоху научно-технической революции. В эпоху технической революции был освоен способ усиления мощности. Теперь же, в эпоху научной революции, осваивается способ увеличения коэффициента усиления мощности. Этот аспект проблемы хорошо изложен в короткой, но очень содержательной книге Б. Г. Кузнецова [2] “Физика и экономика”, где производительность общественного труда и три ее производные по времени представлены как компоненты фундаментального экономического индекса:

В этой же книге Б. Г. Кузнецов пишет: “...исходным показателем цивилизации служит отношение выраженных в каких-то физических единицах сил природы, которые приведены в целесообразное действие и целесообразным образом скомпонованы человеком, к затраченным на это инициирующим силам самого человека. Для получения этого индекса нужно взять энергетическую вооруженность труда, т. е. число киловатт-часов, выделяющихся при процессах, целесообразно контролируемых человеком, деленное на число человеко-часов, на число участвующих в производстве людей или даже на численность населения. При мало меняющемся числе часов использования киловатт-часы можно заменить киловаттами” (стр. 33).

Если коэффициент усиления мощности, т. е. А в формуле Б. Г. Кузнецова, относится к технической революции, то коэффициенты В и С при второй и третьей производной от мощности по времени имеют прямое отношение к интеллектуальным усилиям человечества.

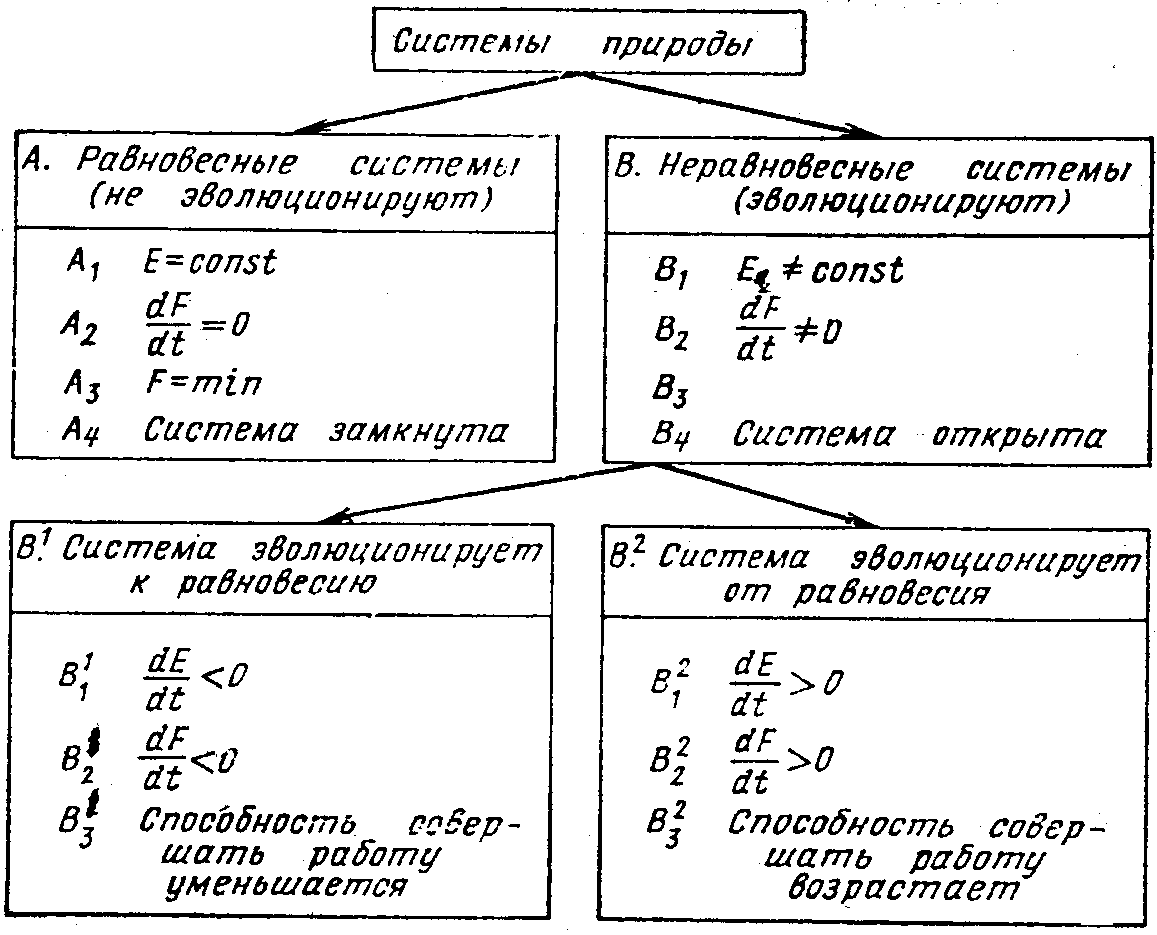
Рис. 1. Классификация систем.

Наша точка зрения на интеллект как на природное явление, которое обеспечивает непрерывный рост мощности на каждый килограмм веса человеческой популяции, полностью совпадает с точкой зрения Б. Г. Кузнецова и позволяет видеть прямую связь между иллюстративным примером Эшби и решением проблемы искусственного интеллекта. Эта точка зрения вытекает как логическое следствие из наших прежних работ по термодинамическим особенностям биологических и социально-экономических систем. В настоящее время почти все согласны, что имеются такие свойства эволюции биологических систем, которые не следуют или не вытекают из закономерностей, которыми мы описываем явления неживой природы. Это отличие иллюстрирует схема, приведенная на рис. 1 [3б].

Эта схема демонстрирует класс систем, которые эволюционируют от равновесия, т. е. системы, у которых способность совершать работу или вызывать изменения в окружающей среде не уменьшается с течением времени. Этот принцип и служит эвристическим признаком для выяснения понятия “цель” в системах с “целенаправленным поведением”.

Настоящая книга посвящена машинному моделированию интеллектуальной деятельности человека, построенной на анализе действий отдельного индивидуума при решении конкретных творческих задач. Это важное и конструктивное направление в современной кибернетике позволяет, не дожидаясь конечных результатов исследований по проблеме построения искусственного интеллекта, получать промежуточные результаты, которые представляют определенный научный интерес и имеют важное прикладное значение. Известно, что в силу определенной сложности предмета, наличия многих междисциплинарных связей, отсутствия методологии исследований, апробированной в широких масштабах, мировая наука пока лишь нащупывает подходы к решению этой проблемы. Книга Е. А. Александрова, обобщающая многие работы автора за последнее десятилетие, освещает один из таких подходов — интегративный или, как его еще называют, естественно-научный подход, основанный на изучении информационной работы мозга и перенесении найденных таким путем принципов в технические системы. Думается, что ознакомление с этим подходом принесет несомненную пользу и будет способствовать выработке достаточно глубокого и строгого взгляда на поднятую автором проблему.

В этом приложении мне хотелось бы обратить внимание на анализ действий коллективного разума, который возникает и доступен прямому наблюдению при формировании и реализации комплексных научно-технических и медико-биологических программ.

К числу таких программ относятся программы создания систем жизнеобеспечения как в малом (для космических кораблей и т. п.), так и в большом (создание системы охраны здоровья для населения всей страны). В таких комплексных программах работают одновременно математики, физики, химики, биологи, экологи, физиологи, психологи, врачи и инженеры самых различных специальностей. В процессе формирования и реализации программы эти отдельные индивидуумы превращаются в целостный коллективный мозг системы. Этот коллективный мозг всех специалистов фиксирует результаты своей деятельности в комплекте рабочей документации на систему и в бесчисленном множестве отчетов, посвященных решению тех или иных научных и технических проблем, связанных с проектированием системы жизнеобеспечения. Не существует одного индивидуума, который может сказать: “Это все сделал я” – существует коллективный мозг, результаты работы которого и превращаются в материальную конструкцию системы. Созданная система жизнеобеспечения является материализованной мыслью коллективного мозга.

Если сделанная система жизнеобеспечения – результат работы этого коллективного мозга, то в чем же вообще состоит процесс коллективного мышления? Оказывается, это процесс синтеза разветвленной логической теории из локальных логических и интуитивных теорий. Очень часто сами разработчики не догадываются о внутреннем содержании своей деятельности по синтезу обобщающей логической теории. Тем не менее, созданная ими система является материальным воплощением этой обобщенной логической теории. Система обеспечивает преобразование заданных входов в заданный выход, а ее математическое описание – преобразование исходных данных (входа) в решение (выход).

В реальной разработке этот процесс создания обобщенной логической теории состоит из выявления накладываемых на проектируемую систему логических условий, которые принадлежат различным областям научной и технической деятельности. Совокупность таких логических условий: физических, химических, биологических, физиологических, медицинских, технических, – выявляется в процессе разработки комплексной программы с помощью листов согласования. Листы согласования, являющиеся документами систем управления комплексными научными программами “Cпутник–Cкалар”, характеризуют систему связей между участниками разработки.

Сама разработка этих машинных систем для планирования и управления процессом разработки систем жизнеобеспечения оказалась пригодной для системы, которая интегрирует всю совокупность научных теорий, используемых при проектировании. Описание систем “Спутник–Скалар” см. в литературе [4–6]. Многие читатели, вероятно, отождествляют понятие “план” с сетевой моделью плана разработки. Сетевая модель плана имеет вид ориентированного графа, но не каждый ориентированный граф соответствует плану. Чтобы сетевая модель плана имела вид ориентированного графа, необходимо содержательное заполнение листов согласования, которые фиксируют все связи, имеющие место между участниками комплексной программы.

При работах по моделированию интеллекта на вычислительных машинах [7, 8] принято отождествлять программу вычислительной машины с термином план. Считают, что подобно тому, как программа управляет поведением вычислительной машины, план управляет поведением человека. Способ формирования и реализации плана, имеющий свои особенности, позволяет, как это показано в [8], говорить о характере личности. Когда в оперативной памяти человека появляется план, то состояние личности характеризуется психологическим термином “появление намерения или желания”. Верно и обратное заключение: возникшее в сознании личности “намерение или желание” влечет за собой появление плана в оперативной памяти личности. Возникновение намерения или желания в коллективе соответствует возникновению некоторого плана. Если процесс возникновения и реализации плана в индивидуальном мышлении скрыт от непосредственного наблюдения, то процесс формирования и реализации плана коллективной работы реализуется документами системы управления комплексной научной программы. Этот процесс гораздо легче наблюдать, если вы работаете в тесном контакте с коллективом руководителей.

Вычислительные машины, которые использовали для моделирования интеллектуальной деятельности в [7, 8], были машинами последовательного действия, а для моделирования коллективного мозга разработки систем жизнеобеспечения нужны параллельные многомашинные комплексы типа ИЛЛИАК-4 или вычислительные системы и среды, которые разрабатываются под руководством Э. В. Евреинова и Ю. Г. Косарева [9]. К этому же классу машин можно отнести полиэдральные сети Г. Крона [11]. Для научной деятельности коллектива характерна параллельность: многие ученые ведут свою работу одновременно. Между параллельными работами существуют связи, предполагающие обмен информацией между параллельными процессорами в машинной модели. Это обстоятельство существенно отличает коллективный мозг от методов работы индивидуального мозга. Тем не менее, мы по-прежнему можем говорить о характере научного коллектива, если рассматривать способы формирования и реализации планов. В отличие от мышления отдельного человека, весь процесс формирования и реализации планов легко наблюдаем через службу сетевого планирования и управления, а также через механизм принятия решений оперативно-руководящей группой. Формирование и реализация комплексных научных программ – это процесс формирования и реализации в металле логической (математической) теории. Процесс превращения отдельных интуитивных и логических теорий в комплексную теорию и оказался основным процессом коллективного мышления.

Основной процесс коллективного мышления – процесс отображения частных логических и интуитивных теорий в обобщенную логическую теорию.

Научный коллектив, который должен будет решить комплексную проблему, представляется (в момент образования) коллективом из разнородных ученых и инженеров, каждый из которых говорит на профессиональном жаргоне своей специальности. Достаточно представить врача и математика, которые впервые встретились для обсуждения будущей совместной работы. Они почти не понимают друг друга, хотя и тот и другой могут быть крупными учеными, каждый в своей области. Выделим то общее, что привело их к участию в комплексной научной программе: они – ученые. Слово “ученый” может пониматься двояко: либо это тот человек, которого “много учили”; либо человек, который может “делать науку”. Поскольку речь будет идти об изготовлении логической теории, то нас будет интересовать второе определение. Мы будем говорить об “ученом” как о конструкторе научной теории. Ситуация, с которой мы имеем дело, формально имеет следующий вид: мы приступаем к работе в комплексной научной программе, не располагая логической теорией; мы закончили работу в комплексной научной программе, когда нужная логическая теория разработана и физически реализована в работающей конструкции. Мы начинаем с утверждения: “формальной теории нет”, а заканчиваем работу утверждением: “формальная теория есть”. Очевидно, что никакой формальной логической непротиворечивой теории, описывающей процесс создания теории, существовать не может. Этот-то процесс формирования логической теории и приходится называть эвристическим. Итак, мы уточнили наше понимание эвристики.

Эвристика – это набор правил по отображению интуитивной теории в формальную (логическую, математическую) теорию.

Можно, следуя за Г. Саймоном [16] говорить, что эвристика – это теория конструирования. Можно привести много других названий: системный анализ, системный подход, общая теория систем и т. п. Мы рассматриваем эту область как теорию коллективного мышления. Не исключено, что знание того, как работает коллективный мозг, позволит, нам лучше понять, как работает индивидуальный мозг.

Изучение основного процесса коллективного мышления мы начнем с некоторой математической аналогии. Возьмем какой-нибудь предмет, например кирпич. Указывая координаты вершин этого кирпича, мы можем записать положение этого кирпича в пространстве. Принимая множество координатных систем, отличающихся друг от друга положением начала координат, масштабами по осям координат, углами, под которыми расположены оси координат, и, используя криволинейные системы координат, мы получим различные формы записи одного, и того же кирпича. Запишем выражение объема этого кирпича во всех системах координат. Очевидно, что вид формулы, выражающей объем одного и того же кирпича, будет зависеть от выбранной нами системы координат.

Вся совокупность формул, выражающих объем, может рассматриваться как совокупность высказываний об одном и том же объекте, но сделанных с использованием различных языков. Если соединить все эти формулы, выражающие объем одного и того же кирпича, знаком равенства, то мы получим правило, которое позволит опознать один и тот же объект, но записанный различными языками. Математический знак равенства в нашем примере означает, что есть один и тот же объект, но описанный в различных системах координат.

В основном процессе коллективного мышления одно и то же явление природы описывается различными языками, зависящими от профессии ученого. Принято думать, что различие в профессиональных жаргонах неустранимо. Тем не менее, это не так. Подобно тому, как математика нашла способ опознавать один и тот же объект, записанный в разных системах координат, может быть найден и способ интеграции профессиональных знаний. Этот способ использует ту же основу, что и математика – мы имеем в виду тензорный анализ. Тензорный анализ, созданный для геометрических нужд, быстро нашел применение в широком круге проблем теоретической физики. В последней он используется для записи законов природы в форме, которая не зависит от точки зрения наблюдателя, т. е. в форме, которая не зависит от выбора системы координат.

Мы не видим оснований для отказа от этого языка, когда переходим от проблем теоретической физики к проблемам биологии, медицины или техники. Мы полагаем, что развитие тензорного анализа в той форме, которую ему придал Г. Крон в “Тензорном анализе сетей”, вполне пригодно для создания универсального языка науки и техники. Эти работы Г. Крона [10, 11], получившие дальнейшее развитие в трудах японской исследовательской ассоциаций прикладной геометрии [12], могут составить базу для успешного решения проблем искусственного интеллекта. Следует сразу же заметить, что термин “сеть”, который введен Г. Кроном, относится к любой инженерной структуре, состоящей из взаимосвязанных симплексов, образующих полиэдр. Если речь идет о структуре из 0- и 1-симплексов, то говорят о 0–1-сети и т. д. до n-сетей. Этот специальный смысл термина “сеть” был потерян, при переводе “Диакоптики”.

Вернёмся к процессу отображения интуитивной теории в математическую или логическую теорию. Следуя положениям Н. Бурбаки, всякую математическую теорию можно представить состоящей из трех составных частей. Эти части составляют своеобразные технические условия на приемку математической теории. Если осуществлять приемку математических теорий по такому же принципу, как в технических системах, то мы обязаны принимать следующие составные части математической (логической) теории: 1. Язык теории. 2. Аксиомы (постулаты, правильные формулы) теории. 3. Правила вывода.

Унифицированная запись большинства разделов современной математики в соответствии с этими техническими условиями и была реализована группой Н. Бурбаки.

Каждой из перечисленных составных частей теории соответствуют “частные” технические условия. Эти условия можно представлять как ответы на вопросы: сколько? и какие именно?

Осуществляя приемку языка теории, мы принимаем его три составные части: 1. Алфавит (список букв и знаков, используемых для написания текстов). 2. Словарь (список слов, т. е. терминов или термов, образованных из букв и знаков алфавита). 3. Формализм (список всех высказываний, образованных из слов или терминов словаря данной теории. Каждое высказывание в стенографической записи имеет вид формулы. Термин “формализм” введен из-за отсутствия подходящего названия для этой составной части).

Общее количество высказываний, образованных из данного словаря, является четным. Четность количества высказываний следует из того факта, что каждому положительному утверждению, высказанному на языке теории, соответствует отрицание этого же утверждения. Таким образом, язык математической теории нейтрален относительно того, что является правильным или неправильным в прикладных теориях. Соответствие правильности или неправильности высказывания относительно физической реальности не является вопросом языка. В силу названного обстоятельства знание математических языков не дает знания того, что считать правильным или неправильным в биологии, физиологии или медицине. Вопрос о соответствии математических формул физической реальности является не математическим вопросом.

Отождествление математической формулы с физической реальностью осуществляется с помощью аксиом постулатов или правильных формул. В математике выбор аксиом является до некоторой степени свободным. Тем не менее, когда речь идет о прикладных математических теориях, то в фиксированных аксиомах теории содержатся законы специальных наук. По этой причине именно второй компонент математической теории – ее аксиомы, и представляет собой в устройстве теории очень важную часть. Как указывалось выше, в чисто математической области фиксация одного из двух противоположных высказываний в качестве истинного и соответствует формулировке аксиом или постулатов. Обнаружение “свободы” в выборе аксиом является исторически сравнительно новым фактом. В истории философии этот факт был известен значительно раньше. Средневековые схоласты довели до высокого совершенства систему логических доказательств. Их блестящие работы незаслуженно забыты и именно потому, что в то время можно было видеть две безупречные логические системы, каждая из которых содержала противоположные выводы. Если логика каждой из этих систем казалась безупречной, то как можно было надеяться на логическое постижение истины?

Фактически схоласты открыли диалектику формально-логических систем. Второй раз этот факт был открыт в области чистой математики Лобачевским. Понятие истины в математике приняло современный вид как непротиворечивость логической системы без всякого отношения к тому, что является истиной в природе. Каждая логическая теория, являющаяся непротиворечивой, при содержательной интерпретации остается верной в границах, которые определяются верностью исходных утверждений или аксиом. За пределами границы, имеющей место для любого содержательного утверждения, всегда наблюдаются факты и явления, которые не следуют из этих аксиом.

Расширилось и математическое понимание термина “теория”. Если до Лобачевского считалось очевидным, что существует одна геометрия, которая базируется на списке аксиом Евклида, то после Лобачевского стали говорить о множестве геометрий, каждая из которых порождается своей системой аксиом. Нетрудно видеть, что, используя один и тот же язык, но фиксируя в качестве аксиом различные наборы высказываний, можно построить много различных теорий, выводы которых могут противоречить друг другу. Противоречивость выводов, относящихся к различным теориям, не нарушает логической непротиворечивости каждой конкретной теории. Этот математический факт, к сожалению, остается неизвестным некоторым физикам. Отождествляя математическую физику с содержанием физики, они еще не привыкли к тому что, существует столько же различных математических физик, сколько существует различных геометрий. Они не могут привыкнуть к тому, что каждое утверждение, верное в одном классе явлений, может быть неверным, если мы переходим к другому классу явлений.

Автору приходилось видеть, как в научных аудиториях воспроизводился известный павловский эксперимент с собаками. И. П. Павлов отобрал группу собак, которые отработали условный рефлекс выделения слюны при виде круга, но не эллипса. На этих же собаках поставили новый опыт, который состоял в том, что в поле их зрения круг переходил в эллипс. Когда собаки не могли отличить круг от эллипса, они давали любопытную реакцию: “сильные” собаки отворачивались, стараясь не видеть противоречащего “факта”, а “слабые” собаки приходили в истерику. Подобное же явление – “закрывать глаза на факты”, если они противоречат логической теории, или бросаться при этом в истерику можно наблюдать у тех физиков, которые не привыкли к понятию истина, принятому в математике.

Расширение списка известных аксиом математической физики, т. е. её законов природы, и уточнение границ применимости для каждой аксиомы, составляют сущность процесса развития науки. Логические теории непротиворечивы в границах данной системы аксиом, в то время как процесс развития математики и науки как целого связан с отрицанием старой системы и утверждением новой системы аксиом, которые имеют силу за пределами старой теории.

Логическая теория является непротиворечивой, если выводимые формулы не противоречат аксиомам теории. Аксиомы теории не ставятся под сомнение. Отрицание аксиом – это не обычное логическое противоречие, а новый вид отрицания, которой и соответствует диалектическому отрицанию. Такое отрицание системы аксиом Евклида не отбрасывает, не зачеркивает геометрии Евклида, а указывает на ограниченность данной теории. Такое отрицание сохраняет старую теорию, создает новую и обе объединяет в высшем синтезе как части более сильной теории. Такое отрицание претерпела и механика Ньютона как часть более сильной физической теории.

Фиксируя объект диалектического отрицания в виде аксиом логических теорий, мы отделяем область диалектики от разговоров на тему об использовании диалектики, указывая модель диалектического отрицания. Приходится сожалеть, что блестящие достижения математической мысли не могут быть по достоинству оценены той частью ученых, образование которых принято считать полноценным и без знания математики. Нет другой области, где понятие истины как истины в определенном контексте является наиболее выраженным. Именно поэтому сильнейшее орудие научного познания действительности, препятствующее окостенению научной мысли, – диалектический метод, вынужден рядиться в новые одежды системного анализа, общей теории систем и т. п.

Вернемся к устройству аксиом логической или математической теории. Мы будем делить аксиомы на две группы: 1. Аксиомы, которые в данной теории всегда правильны. 2. Аксиомы, которые в данной теории правильны в конкретной задаче.

Вторую группу аксиом принято называть условиями задачи. Меняя условия задачи, мы переходим от одних верных утверждений к другим верным утверждениям, но остаемся в рамках одной и той же теории. В тех случаях, когда мы изменяем аксиомы первой группы, мы переходим от одной теории к другой.

При фиксированном языке теории переход от одной теории к другой состоит в изменении системы аксиом первой группы. В прикладной теории этому набору аксиом соответствует система законов природы. При традиционном способе создания математических моделей, когда эти группы аксиом не различают, смена условий может приводить фактически к смене теории. Этот подход игнорирует богатую содержательную историю конкретных наук и приводит к “открытию” уже известных законов. Мне пришлось видеть, как был “открыт” закон действующих масс в химическом эксперименте. Это произошло потому, что сам закон не был строго сформулирован.

Аксиомы вносят асимметрию в множество высказываний, которые можно записать из слов данной теории: множество распадается на два подмножества – подмножество правильных и подмножество неправильных высказываний. Можно сказать, что именно аксиомы превращают нейтральный язык математики в теорию, где не все высказывания правильны.

При постановке конкретной задачи мы пополняем список аксиом, т. е. законов природы, аксиомами-условиями, т. е. утверждениями, которые имеют место в конкретной ситуации. Расширенный список аксиом еще более сужает список высказываний, которые являются правильными. При этом может случиться, что ни одно высказывание не считается правильным. В этом случае говорят, что условия противоречивы. Может быть и так, что множество высказываний удовлетворяет всем условиям. В этом случае принято говорить, что условия недостаточны для получения однозначных предсказаний. Наконец, может случиться, что совокупность аксиом и условий определяет одно и только одно высказывание, которое и является предсказанием теории. В этом случае принято говорить, что условия необходимы и достаточны.

Фактическую проверку решения-предсказания на отсутствие противоречия с аксиомами принято называть решением задачи. Процедура нахождения решения задачи, определяющая правила нахождения предсказания, называется алгоритмом.

Третья составная часть математической или логической теории состоит из правил вывода. Правила вывода математической логики представляют собой символическую запись правил формальной логики, контролирующих непротиворечивость рассуждения. С помощью правил вывода любое предсказание теории может быть приведено к виду, допускающему сравнение с аксиомами теории.

Наш краткий экскурс в устройство математических теорий преследовал цель показать, во что превращаются интуитивные знания отдельных специалистов в процессе проектирования систем. Трудность формирования и выполнения комплексных научных программ состоит в трудности формирования объединенной логической теории, опирающейся на логические условия, принадлежащие различным областям науки и техники. Именно эту трудность и преодолевает коллектив разработчиков. Не всегда это содержание основного процесса создания технической системы бывает известно участникам разработки, но результат их деятельности во всех случаях приближается к созданию формальной теории. Интересно заметить, что в комплексных научных программах создаются логические теории, которые включают десятки и сотни тысяч логических условий. Такой объем научной теории просто не вмещается в отдельную человеческую голову. Обычный человек не может служить предсказывающим устройством даже в логической теории на 100 условий. Кодовое дерево возможных предсказаний содержит 2¹⁰⁰ – 10³⁰ предсказаний. Если бы такой человек существовал и произносил по одному предсказанию в секунду, то он бы закончил перечисление того, что ему известно, через 30 миллионов лет.

Явная невозможность для отдельного человека оперировать с логическими теориями на десятки и сотни тысяч логических условий и порождают сомнение в способности человека. Именно это противоречие между бесконечностью реального мира и ограниченным временем жизни человека – является проблемой, решение которой возможно на пути создания искусственного интеллекта.

ОПЕРАЦИОННОЕ ОПРЕДЕЛЕНИЕ ТЕРМИНОВ ИЛИ СЛОВ В ОБОБЩЕННОЙ ЛОГИЧЕСКОЙ ТЕОРИИ.
ЗАПИСЬ ЗАКОНОВ ПРИРОДЫ

Различие профессиональных языков участников комплексной научной программы порождает первый (но не последний!) барьер – отсутствие общего языка. Даже в области, которая не имеет никакого отношения к науке, можно заметить множество значений такого слова, как корень. Корень в алгебре и корень в ботанике, корень слова и корень зуба... Гипербола литературоведа не имеет ничего общего с гиперболой математика и т. д.

Учитывая, что язык обобщенной формальной теории должен быть пригоден для всех специалистов, предложено использовать в качестве термина название измерительной процедуры. В математике каждому вводимому термину предшествует так называемый квантор существования, который делает законным использование соответствующего термина. В реальной ситуации роль квантора существования возлагается на измерительный прибор. Если измерительный прибор существует, то значение термина определяется отсчетом на шкале или шкалах измерительных приборов. Последовательное применение этого принципа, допускающего написание математического символа тогда и только тогда, когда существует измерительный прибор, исключает множество недоразумений с неоднозначным толкованием слов или терминов. С другой стороны, значение термина также определяется однозначно, ибо прибор в каждый момент времени дает один и только один отсчет. Следует отметить, что хотя принцип операционального определения терминов используется около пятидесяти лет, имеется еще много случаев, когда в математические описания попадают символы, которым не соответствует никакая измеряемая величина.

Принимая соглашение об операциональном определении терминов, мы можем говорить об “экспериментальном пространстве”, где число осей соответствует числу шкал измерительных приборов.

Вслед за У. Р. Эшби такое “экспериментальное пространство” стали называть “фазовым пространством”. Этот шаг отождествления терминов с измеряемыми величинами необходим, но недостаточен.

Любой набор отсчетов на шкалах различных приборов с легкой руки того же У. Р. Эшби стал называться “вектором”, а число осей отождествляться с числом компонент вектора.

В этом вопросе нам пришлось пережить немало неприятностей, так как авторитет У. Р. Эшби сделался препятствием на пути к истине. Мы уже отмечали, что истина в математике и истина в прикладных теориях имеют различный символ. Отождествление терминов с названиями измерительных приборов привело к тому, что два прибора называются по-разному, тогда как измеряют одну и ту же физическую величину. Под влиянием такой ситуации мы сделали вывод, что термин математической теории нужно отождествлять с названием физической величины.

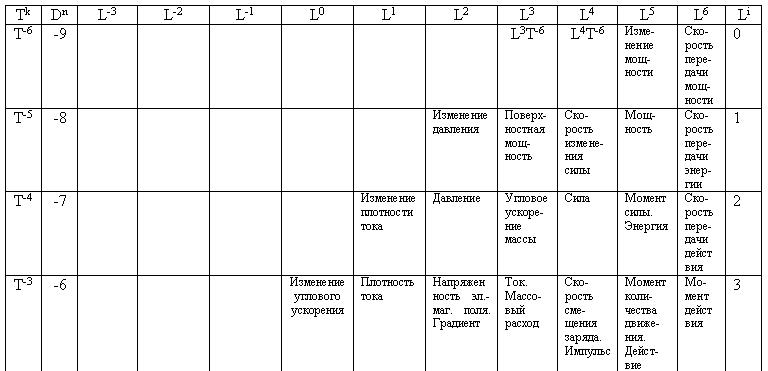
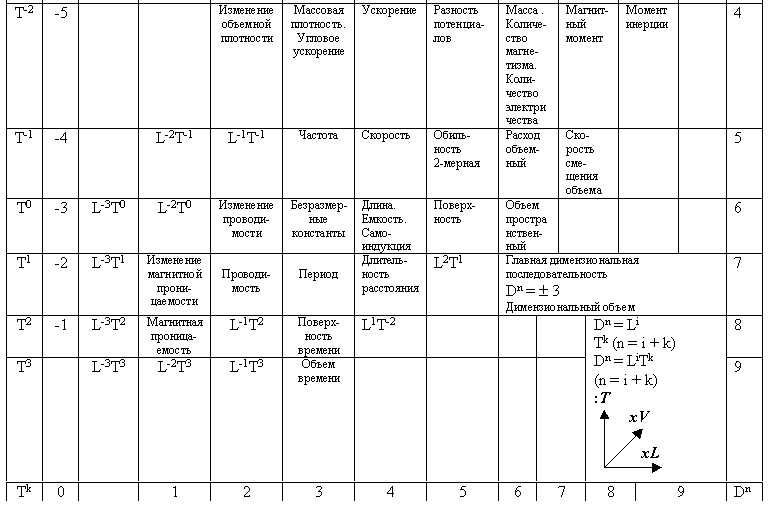
Этот же шаг, но значительно раньше, сделан Дж. К. Максвеллом, а вслед за ним и Г. Кроном. В данном случае возможен вопрос: “Можно ли дать словарь для всех возможных физических величин?”. В таком словаре каждый символ прикладной теории всегда бы соответствовал определенной физической величине. Изучение этого вопроса и привело нас к кинематической системе физических величин, предложенной Р. О. ди Бартини. Эта кинематическая система физических величин использует в качестве основных размерных величин только две: длину [L] и время [T]. Все остальные физические величины, включая массу, считаются производными от этих двух основных и представляются в виде произведений. Любая физическая величина в этой системе представляется общей формулой [L^rT⁸], где r и s – целые числа (положительные или отрицательные).

Вся совокупность физических величин, которые можно измерять, представляется бесконечной таблицей целочисленных степеней длины и времени.

Работы Р. О. ди Бартини [13, 14] подготовили следующий шаг для понимания природы законов физики. Достаточно взглянуть на таблицу кинематической системы физических величин Р. О. ди Бартини, которая дает перечень физических величин, как напрашивается новый вывод: не является ли она таблицей законов природы? Этот вывод – один из наших совместных результатов с Р.О. ди Бартини.

Таблица дает физические понятия, а не математические. Математика имеет контекстно-свободный язык, т. е. её термин допускает много различных интерпретаций. Словарь приведенной таблицы контекстно связан: каждое понятие соответствует одной и только одной физической величине.

Это и позволяет отличать понятие “вектор”, использованное У. Р. Эшби, от понятия “вектор”, которое опирается на таблицу физических величин. Вектор скорости содержит компоненты, которые имеют размерность [L¹T^-1], вектор тока – компоненты которые имеют размерность [L³T^-3].

Если выбрать строчку таблицы, в которой размерность времени нуль, то можно найти все физические величины, имеющие геометрические аналоги. Мы имеем в виду существование величин длина, площадь, объем и т. д. Таблица показывает, что это различные величины, а математика это различие подчеркивает через кванторы существования: из существования понятия длина еще не следует существование понятия площадь.

В таблице понятие “размерность физической величины” используется как термин, который может вводить в заблуждение математика. Понятие размерность в математике имеет совсем другой смысл, что вынуждает нас использовать термины базис или ранг для числа измерении в математических пространствах.

Это смешение физических и математических понятий было замечено японскими исследователями С. Окада и Р. Онодера [12] и А. Д. Мышкисом [15]. Последний пишет:

“Замечание о размерностях. В предыдущем изложении мы, как обычно в математических рассмотрениях, считали все участвующие величины безразмерными. Тогда теория получается более простой; поэтому при действиях с размерными величинами часто в самом начале исследования с помощью выбора характерных единиц переходят к безразмерным величинам, чтобы в дальнейшем только с ними иметь дело. Однако это не всегда удобно.

Система физических величин Р. О. ди Бартини

При действиях с размерными тензорными величинами применяются два различных подхода; об этом иногда забывают, что приводит к недоразумениям уже в линейной алгебре”.

Действительно, эти недоразумения весьма распространены и порождаются тем, что в языке математики не может быть физических величин. Из-за этого обстоятельства происходит разрыв между физическим и математическим описанием. Японские исследователи С. Окада и Р. Онодера остановились на полдороге из-за нецелочисленности размерности заряда, они начали рассмотрение тензоров с одномерного эффинного пространства. Для кинематических величин им удалось отождествить контрвариантные индексы с размерностью длины, а ковариантные индексы с отрицательной размерностью времени. Понятие “частота” оказалось ковариантной величиной относительно изменения масштаба времени и инвариантной величиной относительно изменения масштаба длины. Понятие “ускорение” оказалось тензором, один раз контрвариантными относительно изменения масштабов длин и дважды ковариантным относительно масштабов времени [12]

Построение тензорного анализа на базе аффинной геометрии можно рассматривать как частный случай построения тензорного анализа на базе проективной геометрии, так как аффинная группа является подгруппой проективной группы и характеризуется тем, что переводит бесконечно удаленные точки в бесконечно удаленные. Однако именно из аффинной геометрии заимствован термин аффинор. Если исходить из проективной геометрии, то мы получим термин проектор. При переходе к проективному пространству с инвариантом в виде гармонического или ангармонического отношения четырех точек, мы получаем наиболее естественный ввод всех понятий тензорного анализа. Обобщение одномерного проективного пространства на n-измерений не требует особого рассмотрения.

Поскольку мы будем связывать величины кинематической системы с соответствующими тензорами, сделаем оговорку относительно правил написания индексов. Степень длины (положительная) дает число контрвариантных индексов, которые мы будем писать справа, а отрицательная степень времени дает число ковариантных индексов справа снизу. Для обратных величин индексы пишутся слева и меняются местами: отрицательные степени длины – ковариантны, а положительные степени времени – контрвариантны. При таком расположении индексов любая величина таблицы может быть легко опознана.

Рассмотрим кинематику точки, если уравнение движения последней представлено в виде степенного ряда s(t) = a₀ + a₁t + a₂t² + a₃t³ + …, где s(t) – длина пути, пройденного точкой, a₀ – смещение, a₁ – скорость, a₂ – ускорение, a₃ – изменение ускорения,...

Обращаясь к кинематической системе физических величин, мы видим, что коэффициенты этого ряда есть размерные величины, с общей формулой [L¹T^-n].

Это же уравнение в координатах принимает вид:

s^α(t) = Q^α + Q^α_xβ t^β + Q^α_xβγ t^β t^γ + Q^α_βγδ t^β t^γ t^δ + …,

где s^α(t) – длина пути, пройденного точкой, Q^α – смещение, Q^α_xβ – скорость, Q^α_xβγ – ускорение, Q^α_xβγδ – изменение ускорения, ...., α, β, γ, … = 1, 2, 3.

Нетрудно видеть, что физическая размерность каждого терма есть [L¹T^-n], а коэффициенты этого ряда представляют собою различные физические величины, т. е. различные физические понятия. Эти понятия можно различать по числу и расположению индексов.

Заметим, что в приведенной записи время имеет три измерения, т. е. мы работаем в (3+3)-мире Бартини, а не (3+1)-мире теории относительности. Это различие масштабов времени по различным направлениям здесь закладывается с самого начала, что приводит к ясному пониманию неравенства, “поперечного” и “продольного” времени, которое доставило массу неприятностей физикам начала нашего века.

Обратим внимание и на другой факт. Если заставить индексы пробегать не три, а m значений, то мы будем иметь базис или ранг абстрактных пространств, равный m, но размерность всех величин останется неизменной. Именно этот факт слияния двух различных понятий в один термин “размерность” делал невозможным отличие базиса линейного пространства от размерности физической величины, которая рассматривается в этом линейном (или нелинейном) пространстве.

Рассмотрим кинематику изменения площади во времени:

s^αβ (t) = Q^αβ + Q^αβ.._γ t ^γ + Q^αβ.._γδ t ^γ t ^δ + Q^αβ.._γδε t ^γ t ^δ t ^ε +…,

где s^αβ (t) – величина площади, изменяющаяся со временем, Q^αβ.._γ – скорость изменения площади, Q^αβ.._γδ – “ускорение” изменения площади, ... Q^αβ – начальное значение площади; α, β, γ, δ… = 1, 2, 3.

Каждый коэффициент этого ряда представляет собой размерную физическую величину с общей формулой размерности вида [L²T^-n]. Размерность физической величины не изменится, если индекс будет пробегать значения от 1 до m.

Приведенная таблица физических величин была названа таблицей законов природы. Покажем эту связь в явном виде. Приравняем скорость изменения площади постоянной Q^αβ…_γ = const. Перенесем постоянную в левую часть уравнения Q^αβ.._γ — const = 0. Заменим левую часть одной буквой W^αβ.._γ = 0.

Нетрудно видеть, что это тензорная форма записи закона Кеплера: “Радиус-вектор планеты за равные промежутки описывает равные площади”. Другой закон Кеплера: “Отношение куба радиуса планеты к квадрату периода обращения есть величина постоянная” будет записан в виде W^αβγ··_…δε = 0.

Вообще любой закон физики, который формулируется как закон сохранения, можно записать в подобном виде. Так можно записать законы сохранения импульса, сохранения момента количества движения, сохранения энергии, сохранения мощности и т. д.

Выше мы указывали, что существует столько различных физик, сколько существует различных геометрий: каждому классу физических явлений соответствует своя геометрия. Чтобы отделить физику перемещений и поворотов твердого тела от других классов физических явлений, запишем инвариант этой группы движений. Он имеет вид постоянства расстояния между любыми двумя точками тела.

Его тензорная запись выглядит так: W^α = 0.

Если мы хотим изучать другой класс физических явлений, например гидродинамику несжимаемой жидкости, характеризующуюся инвариантом объема, то следует “забыть” о постулате об инвариантности расстояния между двумя точками, а записать W^α ≠ 0, но W^αβγ_… = 0.

Сравнивая различные “геометрии” с различными “физиками”, можно установить два вида подобия явлений: физическое подобие, когда из таблицы физических величин выбраны одни и те же инварианты, и математическое подобие, которое относится к различным физическим величинам, но система инвариантов находится в подобных соотношениях.

Первый случай подобия можно проиллюстрировать на примере из классической механики. Известно, что сила, масса и ускорение классической механики связаны соотношением f = ma.

Записав это выражение для одной частицы, мы видим, что при переходе к механике k-частиц вид этой формулы не изменяется, так как члены этой формулы размерные величины [F]=[M][LT^-2].

В индексной записи это выражение принимает вид

f_i = m_ia_i.

Мы использовали латинские индексы для того, чтобы отделить число частиц, образующих базис линейного пространства, от индексов греческих, которые дают размерность физических величин.

В приведенном примере не появляются новые физические понятия.

Математическое подобие возможно тогда, когда берутся различные физические величины, но подобие состоит в форме уравнений. Этот случай наиболее распространен.

Естественно, что всякая интуитивная теория использует понятия, которые никак не связаны с таблицей. Наш опыт участия в комплексных научных программах показывает, что каждая техническая (и не только техническая) система хорошо описывается в терминах приведенной таблицы, а экономические понятия, как показано в индексе Б.Г. Кузнецова, требуют весьма удаленных от центра клеток таблицы. Это и естественно, ибо исходная величина есть мощность, а в индекс входят и ее высшие производные. Описание же экономических систем с учетом высших производных требует развития неримановой динамики и еще более сложных “геометрий”.

ИНЖЕНЕРНЫЕ ГРАФИЧЕСКИЕ ЯЗЫКИ КАК МНОГОМЕРНЫЕ ЯЗЫКИ

Традиционное математическое понятие язык определяется как одномерная последовательность букв и знаков. Можно понять причину, которая привела к созданию подобного языка, который правильнее называть “письменной речью”. Последовательность фонем человеческой речи превратилась в последовательность букв и знаков на бумаге. Эта последовательность букв и знаков может изображать математический текст и даже математическое доказательство лишь при условии, что мы знаем, в каком порядке следует читать доказательство. Само понятие порядок нельзя ввести корректно в математический текст, ибо чтение любого текста вообще возможно, если мы знаем порядок, в котором друг за другом следуют буквы. Поскольку о понятиях “порядок” и “беспорядок” высказано много различных мнений, отношение этих терминов к понятию “доказательство” в математике следует когда-нибудь выяснить. Ничего не изменится в этом определении, если понятие “порядок” заменить термином “цепь”, ибо этот термин должен выражать тот же смысл, т. е. следование друг за другом звеньев одной цепи.

По мере того, как изучаемые и создаваемые человечеством объекты становились все сложнее, текстовые описания, сохраняющие все детали, делались все более длинными. Письменная речь стала все чаще заходить в тупик, а на смену ей пришли многомерные языки графического описания: топографические, морские, геологические карты, электронные и электротехнические схемы, строительные и машиностроительные чертежи, структурные формулы химии, фейнмановские диаграммы физики и т. п. Таким же языком планирования комплексных научных программ оказалась сеть.

Совершенно очевидно, что вся эта совокупность “графических языков” рождалась стихийно, по мере того, как люди вставали перед той или иной проблемой адекватного описания. Рождение графических языков связано с особенностями человеческого восприятия: зрение используется неэффективно при чтении текста; скорость восприятия информации по топографической карте примерно в тысячу раз выше, чем при чтении текстового описания. Появление вычислительных систем, потребовавших параллельного ввода данных, выдвинуло проблему графических языков на первый план. Начали говорить о создании “картинной логики”, о машинной переработке “картинки” в “картинку”.

В данном параграфе рассмотрим эти конструкты как новые понятия, которые имеют две стороны: одна касается физической реальности, а другая – абстрактных символов, удобных для математической формализации. Располагая такими графическими языками во многих областях науки и техники, мы совершаем различные попытки связать их с математическим описанием. Машинное проектирование технических систем во всех случаях связано с такими описаниями.

Рассмотрим в инженерных графических языках тот их компонент, который касается физической реальности. Одним из таких понятий является понятие сети, введенное Г. Кроном для описания различных электромеханических систем. Элементами сети являются катушки, которые не следует смешивать с “катушками индуктивности”, используемыми в радиотехнических схемах. Катушка у Крона является элементом схемы, имеющим импеданс и рассеивающим мощность. Включение катушек в сеть осуществляется с помощью безымпедансных соединительных проводов. Безымпедансные провода отождествляются с узлами.

Вид электрической схемы весьма напоминает математическое понятие “граф”, что и привело к попытке заменить инженерное понятие “сеть” математическим понятием “граф”. Однако такая замена привела к серьезным недоразумениям. Причина их состоит в том, что свойства математических графов и электрических сетей весьма различны. Поведение электрической сети существенно зависит от характера электромагнитного поля, которое окружает электрическую сеть и взаимодействует с ней. Это электромагнитное поле, которое окружает электрическую сеть, существенным образом входит в теорию электрических сетей, но его изображение отсутствует на графе. Попытка создать теорию электрических сетей со сложным комплексом электромагнитных явлений, окружающим сеть, только на основании видимого графа, – является неудачной попыткой.

Возьмем топографическую карту, на которую нанесена боевая обстановка. Совершенно очевидно, что боевая обстановка является существенным элементом в схеме принятия решений. Представим себе теоретика в области военного искусства, занятого построением теории ведения боевых действий на основании только топографических карт и игнорирующего имеющуюся боевую обстановку. Если отождествить топографическую карту с графом, а боевую обстановку с окружающим сеть электромагнитным полем, то можно представить себе вид граф-теории, которая игнорирует половину исходных данных.

Приведем другой пример. В театральных постановках иногда употребляются люминесцентные краски. При освещении дневным светом мы видим одну картину, а при освещении ультрафиолетовым светом – совсем другую. Этот пример служит иллюстрацией того, что реакция сети существенным образом зависит от вида падающей электромагнитной волны.

Возвращаясь к топографической карте как графическому языку изображения местности, следует отметить, что различные люди, рассматривая одну и ту же топографическую карту, видят разные вещи. Если один зритель, который обучен топографии, видит все складки местности своим “внутренним взором”, то в сознании другого зрителя, не обученного топографическому языку, эта картина не возникает. “Внутренний взор” инженера связан с символическим языком электрической сети; у теоретика в области математических графов он отсутствует.

Эта длинная сентенция относительно графических языков преследует одну цель –показать, что они имеют следующие направления: 1) наименьшим количеством знаков выразить как можно большее содержание; 2) использовать достаточное количество знаковых элементов для указания различий между сходными вещами. Эти явления как свойство интеллекта уже давно отметил Монтескье: интеллект проявляется в умении видеть общее в различном и различие в подобном. Понятие “дом” у инженера-строителя ассоциируется с множеством комплектов рабочих чертежей: каждый дом в комплекте рабочих чертежей имеет свои особенности. Заменить все эти дома одним символом –значит лишить себя возможности понять тонкие различия между разными домами.

Обращаясь к графическим языкам инженерных наук, мы хотим решить следующий вопрос: всегда ли различные графические изображения соответствуют различиям в физической реальности? Нет ли таких свойств физической реальности, которые имеют различное графическое изображение, но представляют собой описание одного и того же объекта физической реальности?

Простейшим примером такого рода является топографическая карта: она может быть дана для одной и той же местности, но в разном масштабе. Точно такая же ситуация возможна и для рабочих чертежей дома: они могут быть выполнены в разных масштабах, но в результате будут построены одинаковые или тождественные дома. В этих случаях существует такое преобразование чертежей или топографической карты, которое совмещает два изображения.

Более сложный случай – рассмотрение карт аэрофотосъемки одного и того же участка местности, но снятых с различной высоты и под разными углами. В этом примере заранее известно, что речь идет об одном и том же объекте, но все его изображения имеют различный вид. Можно показать, что при некоторых условиях (относительно характера отснятой местности) также существует преобразование карт аэрофотосъемки, которые совмещает два изображения. Возможность совмещения двух изображений одного и того же объекта следует из того, что это различные изображения одного и того же объекта. Приведенные примеры показывают, что действительно встречаются ситуации, когда различным графическим изображениям соответствует один и тот же объект физической реальности. Эти ситуации можно отождествить с логическим исследованием, которое было выполнено в математике.

Математики изучали поведение неизменного математического объекта (например, отрезка, плоской или пространственной фигуры, замкнутой кривой и т. д.), который записывается в различных системах координат, и его математическая запись имеет различный вид, но сам объект остается неизменным. Его принято называть инвариантом, а внешний вид его записи в той или иной системе координат – его проекцией в частную систему координат. Вся совокупность проекций одного и того же объекта в допустимые системы координат образует понятие группы, а правила перехода от записи в одной системе координат к записи в другой системе координат – понятие преобразования. Вся совокупность перечисленных понятий и образует новое понятие “тензор”, как группа преобразований с инвариантом.

Приведенное определение понятия “тензор” можно использовать в двух направлениях: группа может иметь различные инварианты при неизменных преобразованиях или различные преобразования при неизменном инварианте. В первом случае одна группа будет отличаться от другой инвариантами, а во втором –преобразованиями. Если в качестве инвариантов используются физические величины из таблицы физических величин Р. О. ди Бартини, то различным группам соответствуют разные классы физических систем. Поскольку понятие “физическая величина” не является математическим понятием, то существует различие между физическим и математическим понятием тензора. Это различие было замечено и использовано Г. Кроном в его тензорном анализе сетей. Для Г. Крона инвариантное преобразование электрической сети связано с группой, характеризуемой инвариантностью мощности, а способ соединения элементов в сеть – вид преобразования, допускаемый этой группой.

Если исходным понятием теории является граф, то изменение способа соединения элементов в графе есть переход к другому графу. Не существует понятия эквивалентный граф, если не использован инвариант некоторой физической величины. Физическая величина связана с физическим понятием размерность, в то время как конфигурация сети, представляемая графом, дает математическое понятие числа суммируемых элементов. Это число обычно связывают с “размерностью линейного пространства”. Мы уже ранее отметили, что для числа суммируемых элементов используется термин “базис” или “ранг” линейного пространства, который никакого отношения к размерности физической величины не имеет. Число катушек в сети Г. Крона определяет число уравнений и базис линейного пространства (для линейных сетей или для 1-сетей).

Переход от одной конфигурации сети к другой конфигурации, т. е. к другому способу соединения тех же элементов безымпедансными проводниками, может изменять базис или ранг линейного пространства, но не выводит новую конфигурацию из группы, определяемой инвариантом мощности. В обычных курсах линейной алгебры линейные пространства считаются изоморфными тогда и только тогда, когда они имеют одно и то же число компонентов базиса или ранга. Это и дает возможность увидеть различие между группой линейных преобразований Г. Крона и группой линейных преобразований линейной алгебры.

Нахождение элементов тензора преобразования Г. Крона оказывается возможным тогда и только тогда, когда мы сравниваем две сети, представленные графическим языком инженера. Достаточно обозначить эти сети символами А₁ и А₂ – как вид тензора преобразования одной сети в другую найти будет невозможно. Отсутствие этого графического многомерного языка, вызванного первой тенденцией развития языка математики, закрывает дорогу к новым результатам, которые могут быть получены при использовании многомерных инженерных графических языков.

Инженерные графические многомерные языки могут применяться и в математике. Если взять математический текст и заменить в нем все высказывания и все формулы символом , а все связи между высказываниями и формулами символом , то любой математический текст превращается в ориентированный граф. Поскольку любая математическая теория может быть заменена графом, то мы получаем возможность сравнивать различные математические теории по виду представляющих эти теории графов. В каждой математической теории, представленной графом, можно выделить три типа формул или высказываний. К первому типу отнесем формулы, из которых исходят логические связи, но в некоторые не входит ни один предшествующий результат, т. е. изображение вида

Этот тип формул соответствует АКСИОМАМ логической теории. Ко второму типу отнесем формулы (высказывания), в которые ВХОДЯТ предшествующие результаты, но из никаких последующих результатов не выводится, т. е. изображение вида

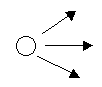
Этот тип формул соответствует выводам из логической теории.

Наконец, к третьему типу отнесем формулы, в которые входят предшествующие результаты и из которых следуют последующие результаты или формулы, т. е. изображение вида

Этот тип формул соответствует промежуточным результатам или процессу доказательства.

Имея графическое представление логической теории, можно говорить об объединении множества логических теорий в общую логическую теорию, соединяющую все исходные аксиомы и все выводы. Именно такое объединение локальных логических теорий в общую логическую теорию и составляет сущность комплексной научной программы, интегрирующей знания специалистов из различных областей науки и техники. В системах жизнеобеспечения общее количество аксиом, т. е. исходных посылок, соответствует нескольким тысячам. Их соединение в логическую теорию систем жизнеобеспечения и достигается с помощью другой сети, которая является символическим изображением плана.

Создание логических теорий на сотни и тысячи логических условий, относящихся к различным разделам науки и техники, составляет процесс конструирования так называемых “сложных систем”. Теория конструирования и теория синтеза логических теорий представляют собой лишь различные названия одного и того же процесса проектирования.

Организационные трудности в создании комплексных научных программ можно видеть по объемному макету целевой организации, порождаемому использованием систем “Спутник–Скалар” (рис. 2).

На макете представлен план, имеющий вид сети в основании конструкции организации, над ним возвышается иерархическая структура организации. Каждая оборванная нитка на макете соответствует организационной неурядице или организационному “сбою”. Формирование и эволюция такой организационной структуры потребовали более основательного знакомства с тензорным анализом сетей, частным случаем которого является описание подобных структур.

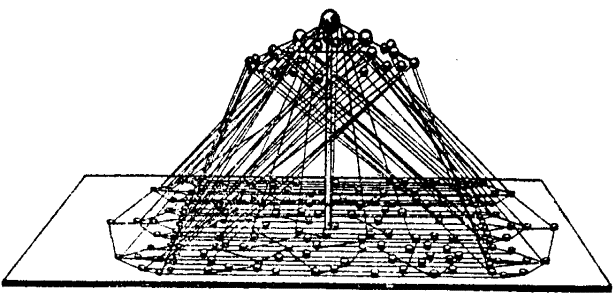
Приведенный макет организации дает некоторое представление о характере связей в сравнительно небольшой организации (около 200 чел.).

Установление логических связей между частными или локальными логическими теориями достигается с помощью “листа согласования”, являющегося документом в системах “Спутник–Скалар”.

В настоящее время все возможные направления развития современной математики можно представить с помощью двух универсальных математических языков: языка теории множеств или языка геометрии. Поскольку эти два языка эквивалентны, а современная математика предпочитает язык теории множеств, то представляется логичным использовать язык геометрии для прикладных теорий. Язык теории множеств остается контекстно свободен, а язык геометрии может быть контекстно связан с прикладными теориями. Контекстно свободный язык теории множеств не будет связывать свободы математического мышления в области чистой математики (развитие которой является очень важным). Язык геометрии, в соответствии с деятельностью Японской ассоциации прикладной геометрии, становится связанным с проблемами инженерного проектирования.

Интересно отметить, что, используя для приложений язык геометрии, мы используем для развития прикладных теорий эрлангенскую программу Ф. Клейна. Различные классы физических явлений и соответствующие этим классам явлений технические системы могут быть поставлены в соответствие с различными группами преобразований. Общая теория физических и технических систем использует в виде направляющего стального каркаса теорию групп. Каждая группа в соответствии с программой Ф. Клейна порождает свою геометрию. Различие геометрий становится различием классов физических явлений и одновременно различием классов технических систем. Наоборот, технические системы подобны, если являются представителями одной и той же группы. Каждый класс физических явлений отождествляется с определенным набором инвариантов, а это приводит к выводу, что различных физик ровно столько же, сколько различных геометрий, т. е. столько же, сколько существует различных наборов инвариантов из таблицы физических величин Р. О. ди Бартини. Подобно тому, как различные частные геометрии объединяются в современную геометрию, различные частные физики объединяются в современную физику. Нельзя одному человеку построить все здание физики. Эти задачи подобны друг другу и требуют для своего строительства всей науки на протяжении всей последующей истории человечества. Так же как истины геометрии остаются в золотом фонде человечества, новые логические теории, которые будут создаваться, перейдут в золотой фонд комплекса машинных информационных систем, т. е. в искусственный интеллект человеческой популяции. Дорогу в этом направлении нам открывает переход одномерного языка традиционной математики к многомерным языкам, порожденным практикой инженерного проектирования технических и организационных систем. Этот язык получил свое точное определение именно в тензорном анализе сетей Г. Крона, который может рассматриваться только как первый шаг на пути к полиэдральным сетям.

НАУЧНОЕ ОБЪЯСНЕНИЕ И НАУЧНОЕ КОНСТРУИРОВАНИЕ

Этот параграф посвящен различию между ученым-наблюдателем и ученым-конструктором. Различие до некоторой степени условно, но в рамках комплексных научных программ можно наблюдать и крайности. Ученый-наблюдатель представляет собой первую крайность: его задача – установить закон наблюдаемого явления. В этом случае его поведение определяется правилами объективности: ничего субъективного, ничего, чем я как личность могу исказить результаты наблюдения. Результат деятельности ученого-наблюдателя состоит в создании теории, из которой следует, т. е. выводится нечто наблюдаемое в исследованном классе явлений. Конечная цель исследователя состоит в установлении закона, т. е. инварианта в наблюдаемой группе явлений. Гипотеза, которой руководствуется исследователь, состоит в том, что закон существует, но еще не открыт, не установлен. Этот закон не может быть навязан природе, он независим от мышления исследователя. После установления инварианта или закона данного класса явлений можно говорить, что часть явлений можно наблюдать и их наблюдение не находится в противоречии с установленным законом, а часть явлений нельзя наблюдать, так как они вступили бы в противоречие с обнаруженным законом.

Открытый исследователем закон позволяет делать предсказания, но только в том классе явлений, который характеризуется установленным инвариантом.

Ученый-конструктор не преследует цели открывать новые законы природы; его задача – использовать известные законы природы для удовлетворения тех или иных потребностей человека или человечества в целом. Исходными данными конструирования являются идеи и инварианты известных законов, а целью – нахождение инженерной структуры, которая использует минимальный объем пространства и минимальное количество “железок” для удовлетворения той или иной потребности.

Таким образом, можно различать две разные логики: логику объяснения и логику конструирования. Логика объяснения состоит в указании того, что можно наблюдать при заданных инвариантах, логика конструирования – в выборе необходимых инвариантов, которые делают материальное воплощение идеи наблюдаемым, т. е. материальное воплощение – физически реализуемым.

Конструктор начинает работу с идеи, а заканчивает ее материальным воплощением идеи в работающей конструкции. Исследователь начинает работу с материальным воплощением работающей конструкции природы, а заканчивает идеей, которая принимает вид закона или сущности, характеризующей изученную конструкцию. Этим различным по своему характеру приемам соответствуют две философские концепции: от природы к идее и от идеи к природе. Синтез обеих концепций, сохраняющий достоинства каждой и лишенный недостатков, нашел свое выражение в утверждении, это задача состоит не только в объяснении мира, но и в перестройке его. Строительство нового мира природы, который лучше удовлетворяет потребностям человека и человеческой популяции в целом, опирается, с одной стороны, на познание законов природы, а с другой – на идеи, которые можно воплотить в материальные конструкции нового мира.

Итак, ориентация логики конструктора на формирование нового, более благоустроенного мира, порождается потребностями. Обычная логика рассматривает понятия потребность и возможность как полярные противоположности. Диалектическая связь этих понятий имеет традиционный для диалектики вид: всякая удовлетворенная потребность есть новая или возросшая возможность, всякая новая или возросшая возможность воспринимается как потребность.

Можно высказать следующее утверждение: каждая потребность может быть выражена в терминах роста той или иной возможности. Всякий рост возможности человеческой популяции может быть выражен в терминах той или иной потребности.

Логика конструирования, опирающаяся на идеи удовлетворения тех или иных потребностей, опирается в то же время на идеи, обеспечивающие рост возможности человеческой популяции. Верно и обратное утверждение: рост возможности человеческой популяции невозможен без идей и механизма их воплощения в материальные конструкции.

Нетрудно видеть, что логика исследователя находится в противоречии с логикой конструктора: первый заканчивает свое исследование запретом, т. е. утверждением о невозможности, второй – лишь при наличии идеи, утверждением – это возможно.

Все законы природы, как видно из таблицы, являются запретами в группах явлений природы и перестают быть запретами за границами этих групп.

Отождествим понятия “возможность” и “производительность труда”. В этом случае понятие “рост возможности” будет соответствовать понятию “рост производительности труда”. Только невежественный человек может сомневаться в том, что закон роста производительности труда не является объективным законом, который управляет ходом истории человечества. Наличие объективного закона истории свидетельствует о том, что человек господствует над природой только в средствах, а в своих целях он скорее подчинен ей. Отдельный индивидуум или группа может развивать бурную деятельность в направлении замедления роста производительности труда, но это исключение никак не повлияет на общий ход исторического процесса. Важно заметить, что осознанная потребность и воспринимается человеком как цель.

Приведенный объективный закон истории и выражается компонентами фундаментального экономического индекса Б. Г. Кузнецова. Этот индекс есть не что иное, как разложение имеющейся в распоряжении человеческой популяции мощности в ряд Тейлора, коэффициенты которого являются размерными физическими величинами. Поскольку три высших производных от мощности по времени положительны, можно сформулировать:

Мощность (физическая величина, имеющая размерность [L⁵T^-5]), отнесенная на килограмм живого веса людей, не уменьшается в ходе исторического развития человечества.

Это утверждение можно рассматривать как эвристический принцип, из него следуют или выводятся различные виды потребностей или целей, которые ставят перед собой люди в их совокупности.

Отождествляя понятие “возможность” с понятием “мощность”, мы должны рассмотреть некоторые определения к термину “возможность”, образующие некоторую иерархию возможностей:

1. Потенциальная возможность – полная величина мощности, потребляемая популяцией или ее частью.
2. Техническая (или физическая) возможность – величина полной потребляемой мощности, умноженной на коэффициент совершенства технологии, т. е. на обобщенный коэффициент полезного действия машин и механизмов, соответствующая технической скорости выпуска продукции.
3. Экономическая возможность – величина технической возможности, умноженная на коэффициент обеспеченности выпускаемой продукции потребителем, т. е. на коэффициент качества плана. Физический выпуск продукции, которая не обеспечена потребителем, это физическая работа, не получающая общественного признания в качестве труда.

Этот поток продукции и образует долю, снижающую коэффициент качества плана от единицы. Таким образом, экономическая возможность – это величина технической возможности, уменьшенная на величину выпуска, который не обеспечен потребителем.

Рассматривая только три определения, мы не используем таких определений возможности, как, например, этическая, социальная и политическая, т. е. мы учитываем, что рассматриваемая теория имеет границы применимости. Теория имеет тот же вид, что и теория движения несжимаемой жидкости: она тем справедливее, чем менее уклоняется описываемая жидкость от постоянства величины объема.

Вышеприведенные определения мы давали в соответствии с требованием операциональности определений каждого термина, предъявляемым к теории вообще. Отождествление понятий “возможность” и “мощность” позволяет говорить о полной возможности или полной мощности, которая имеется в распоряжении человеческой популяции. Такое рассмотрение полной мощности, которой располагает человечество в целом, предпринимается в рамках экономико-географических исследований Г. Бешем [17] или в рамках экологического подхода Г. Т. Одумом [18]. Это далеко не новый подход, а его подлинным основоположником может считаться С. А. Подолинский [19]. История этого вопроса изложена в работах [20–22].

Несколько уточним понятие “возможность”. Допустим, что груз весом 750 кг нужно поднять на высоту в 10 м. В распоряжении имеется бензиновый двигатель, приводящий в движение подъемный механизм (лифт). Рассматривая наше устройство с точки зрения потребления бензина, можно обнаружить, что количество энергии, выделяющееся в единицу времени при сгорании бензина, соответствует мощности в 10 л. с. (1 л. с. = 75 кгм/с). Если бы вся мощность сгорающего бензина превращалась в полезную работу подъема груза, то вся работа была бы сделана за 10 с.

Мощность сгорающего бензина представляет собой потенциальную возможность. Ее величина образует некоторую часть полного потока энергии, получаемого человеческой популяцией.

С учетом трения и бесполезных потерь в двигателе и подъемном механизме фактическая мощность, т. е. техническая или физическая возможность, оказывается равной 20% потенциальной возможности. Таким образом, техническая мощность механизма составляет всего две лошадиные силы, и совершение работы по подъему груза требует времени не 10, а 50 с.

Перейдем к последнему из рассматриваемых определений термина “возможность”. Если потенциальная возможность определялась как полный поток энергии, а техническая возможность – с учетом коэффициента совершенства технологии, то экономическая возможность требует введения нового понятия.

Определим понятие “рынок” как способ общественного производства, при котором сначала выполняется работа по выпуску продукта, а потом ищется потребитель результата сделанной работы.

Определим понятие “план” как способ общественного производства, при котором сначала ищется потребитель результата сделанной работы, а потом выполняется работа по выпуску продукта. Таким образом, понятие “план” означает, что результат каждой работы

в обществе обеспечен потребителем. Понятие “труд” определяется в политической экономии как общественно-полезная деятельность, т. е. такая деятельность, результат которой получает общественное признание через потребителя. Измерителем качества плана может служить величина товарных запасов, которая не имеет потребителя.

Можно заметить, что социальные системы с анархией производства не полностью используют возможности общества, так как имеют низкий или колеблющийся коэффициент качества плана. Эти системы исторически обречены – им на смену идет плановая экономика.

Три использованных определения термина “возможность” достаточно хорошо характеризует некоторые типы целей.

1. Научные исследования и последующие конструкторские работы могут быть ориентированы, т. е. иметь целью создание и реализацию новых источников мощности. Так в истории человечества осваивались мощности домашнего скота, ветра, падающей воды, каменного угля, нефти, газа, ядерной энергии и т. п.
2. Научные исследования и последующие конструкторские работы могут иметь целью создание новых технологических процессов, которые отличаются от ранее известных более высоким коэффициентом совершенства технологии. Эти работы и соответствуют термину “техническая революция”.
3. Научные исследования и последующие конструкторские работы могут иметь целью совершенствование системы управления общественным производством, т. е. ориентированы на повышение коэффициента качества плана. Идеальное общественное устройство предполагает, что ни одного человека в обществе не принуждают к выполнению никому не нужной работы. Это направление научных исследований по совершенствованию системы управления общественным производством и названо важнейшим в решениях XXIV съезда КПСС.

Вернемся к проблеме искусственного интеллекта и разума человеческой популяции на новом уровне рассмотрения. Научно обоснованное управление конструированием будущего должно опираться на результаты научных исследований во всех областях науки, т, е. на интегрированные возможности всей науки. Эти научные данные находятся в одном месте, а решения принимаются в другом. Чтобы избежать одностороннего суждения экспертов, мы должны иметь возможность использовать интеллектуальное богатство человеческой истории для принятия практических решений. Классическое противоречие между ограниченными знаниями одного лица и знаниями человечества может быть разрешено созданием комплекса машинных информационных систем, ориентированных на процесс конструирования будущего, на процесс активного формирования будущего человечества. Эту задачу можно решить только в рамках комплексной научно-технической программы, разработка которой стала исторической необходимостью.

Научные дисциплины и направления получают названия, которые объединяют термин области исследования и окончание “логия” – учение. Процесс конструирования или проектирования будущего не относится к разряду исследований потому, что его результат представляет собой материальную конструкцию, ведущую себя в соответствии с замыслом конструктора. Теория конструирования или проектирования, соединяющая логическую структуру математической теории с физической реализуемостью, должна иметь определенное название. Г. Саймон предложил для этой области название “наука об искусственном”. Мы предлагаем термин “проектология” (наука о проектировании будущего). Ранее мы предлагали перейти от термина аффинор к термину проектор, имея в виду, что класс проективных преобразований шире, чем класс аффинных преобразований. Однако это было только одной из причин введения нового термина, теперь мы встретились со второй: понятие “проектор” ассоциативно связано с проектированием систем и проектированием будущего.

Выше тензорный анализ рассматривался как раздел математики, который позволил записывать некоторые объекты в форме, которая не зависит от выбора системы координат. Физическая интерпретация понятийного аппарата тензорного анализа, которая была дана Г. Кроном, превращает математическую теорию в инженерную теорию и требует изменения названия. Эту теорию проектирования, объединяющую математический аппарат тензорного анализа с физикой – анализом размерности и с инженерным графическим языком сетей, мы предлагаем назвать проектным анализом.

Учитывая, что каждый конструктор системы может иметь свою особую точку зрения на проект системы, будем индивидуальную точку зрения конструктора называть проектором, а предлагаемое конструктором техническое решение – частной проекцией системы данного типа в частную систему координат предлагаемого технического решения. Вся совокупность возможных проектов будущей системы образует группу, а частные технические решения – проекцию инварианта группы в конкретную систему координат. Инвариантом группы для проектируемых систем может быть тот или иной (или несколько) инвариантов из таблицы Р. О. ди Бартини. Это представление весьма полезно для исключения иллюзии конструкторов относительно единственности технического проекта системы. Конструкция коллективного мозга, что известно каждому участнику комплексных научных программ, и состоит в использовании большого числа таких проекторов, образующих иерархию целевых руководителей. Весь коллектив разработчиков, осуществляющих конструирование сложной технической (или другой) системы, связанный в целое (листами согласования), мы и будем отождествлять с проектом пли программой. Именно эту структуру мы и демонстрировали в макете целевой организации.

Развитие проектологии может быть успешным, если классы проектируемых систем можно будет отождествлять с вариантами таблицы физических величин. Это означает, что существует связь между целями в технических системах и инвариантами физических величин.

Эта связь превращает исследователя в конструктора.

ОПРЕДЕЛЕНИЕ ЦЕЛЕЙ ТЕХНИЧЕСКИХ СИСТЕМ ЧЕРЕЗ ИНВАРИАНТЫ ФИЗИЧЕСКИХ ВЕЛИЧИН

Понятие “движение” в геометрии связано с представлением об инварианте, т. е. с такой характеристикой перемещаемого или изменяемого объекта, которая остается неизменной. Классическими инвариантами движений в геометрическом смысле являются длина (“расстояние между двумя точками абсолютно твердого тела”) и объем. Геометрическое перемещение ориентированного отрезка или вектора может осуществляться с сохранением величины и направления. Такое перемещение принято называть параллельным переносом. Эквивалентность или инвариантность вектора при перемещении параллельным переносом настолько очевидна, что можно считать: инвариант и параллельный перенос – два названия одного и того же вектора. Это особенно ярко выражено, если осуществлялся не перенос вектора, а перенос начала координат, т. е. мы имеем дело с тем же самым вектором, но записанным в координатах новой системы. Классические работы Риччи и Леви-Чивитта, которые привели к обобщению понятия параллельный перенос или, как мы убедились выше, к обобщению понятия инвариант, и заложили основы современного тензорного анализа. Это позволяет говорить о движении в геометрическом смысле, как о преобразовании координат с инвариантом. Прежде чем говорить об инвариантах в технических системах, рассмотрим некоторые инварианты геометрических преобразований. Это позволит лучше уяснить идеи тиринг-топологии Г. Крона как идеи группы преобразований равновеликих фигур с разрезом и перестройкой конфигурации фигуры, но с инвариантом.

Вернемся к классическому геометрическому определению движения в той форме, которую хорошо выразил Г. Вейль: “Один из способов описания структуры пространства, которому отдавали предпочтение Ньютон и Гельмгольц, состоит в использовании понятия конгруентности. Конгруентные части пространства V и V' – это такие его части, которые можно заполнить одним и тем же твердым телом в двух его положениях... очевидно, что конгруентные преобразования образуют группу, являющуюся подгруппой группы автоморфизмов. Если говорить подробнее, ситуация такова. Среди преобразований подобия существуют такие, которые не изменяют размеров тела; отныне мы будем называть их “движениями” (Г. Вейль. Симметрия, М., “Наука”, 1968, стр. 70).

Рассмотрим физический пример. Допустим, что у нас есть десять кирпичей, разложенных рядом. Они займут некоторый объем. Теперь изменим ситуацию. Сложим эти кирпичи друг на друга столбиком. Хотя положение кирпичей изменилось, величина объема, которая заполняется этим десятком кирпичей, остается неизменной. Величина объема, занимаемая не одним твердым телом, а десятком кирпичей, является инвариантом. Можно говорить о конгруентности в этом новом смысле и называть движениями и такие изменения конфигурации системы. Однако говорить о том, что движения образуют подгруппу в группе преобразований подобия, уже нельзя. Это группа преобразований равновеликих фигур, сохраняющая величину объема, но допускающая членение величины объема на подобъемы. Саму операцию членения и склеивания кирпичей нужно рассматривать как новую группу преобразований, которую ввел Г. Крон.

Если группа автоморфизмов объединяет фигуры, подобные по форме, то группа преобразований Г. Крона объединяет конфигурации, равные по величине. Такую же операцию разрезания (отсюда и тиринг-топология) можно проделать с листом бумаги, разрезая его на части и раскладывая произвольным образом. Инвариантом этой группы будет величина площади. Если объем кирпичей может быть задан трилинейной формой, остающейся инвариантом при всех размещениях кирпича, то площадь листа бумаги может быть задана билинейной формой, остающейся инвариантом при всех разрезах и размещениях листа бумаги. В общем случае группу обобщенного движения можно задать инвариантом полинейной формы, где величиной, остающейся неизменной, может быть любая величина из системы Р. О. ди Бартини. Частным случаем перекладываемых “кирпичей” могут служить “кирпичи мощности”. Сети Г. Крона образуют группу, инвариантом которой является величина мощности. Сети считаются эквивалентными тогда и только тогда, когда существует неизменная величина мощности. Только низкая математическая культура могла породить такую дискуссию, как дискуссия о роли инварианта мощности в эквивалентном преобразовании электрических сетей. Если исключить этот инвариант, то теряет смысл понятие эквивалентность.

Для восстановления исторической истины следует отметить, что именно Г. Вейль подал Г. Крону мысль об использовании многомерных пространств для построения теоретической электротехники. Еще в 1926 г. Г. Вейль писал: “Представим себе сеть проводников постоянного тока, состоящую из отдельных однородных проводников, разветвляющихся в узловых точках, и назовем “точкой” произвольное распределение тока, которое сообщает каждой проволоке S силу тока I_s. В такой системе имеют силу законы евклидова пространства с центром в О и такого количества измерений, сколько есть проволок в сети. При этом центральная точка О характеризуется отсутствием тока, в ней исчезают все силы тока I_s, а под квадратом расстояния “точки” от центра следует понимать количество джоулевой теплоты, выделяемой токами за единицу времени. Эта изоморфия вовсе не носит характера игры, ибо благодаря ей простые и важные геометрические понятия ставятся в соответствие с простыми и важными, касающимися распределения тока в сети, понятиями физики”. (Г. Вейль. О философии математики. М., Гостехиздат, 1934, стр. 55–56).

Нетрудно видеть, что в описании Г. Вейля присутствуют только некоторые простейшие понятия физики постоянных токов. Эту программу Г. Вейля – установить изоморфизм между простыми и важными понятиями геометрии и такими же простыми и важными понятиями физики – и реализовал в течение 38 лет Г. Крон, поддерживая личные контакты с Г. Вейлем, Джоном фон Нейманом, Освальдом Вебленом, Полем Ланжевеном, Банешем Хоффманом и Альбертом Эйнштейном. В процессе реализация этой программы, активно поддерживаемой друзьями из Принстона, Г. Крон обнаружил, что для более или менее адекватной геометрической картины явлений в электрических вращающихся машинах необходимо использовать нериманову геометрию и работы по общей теории гравитационного и электромагнитного поля. Адекватная геометрия динамики вращающихся электрических машин оказалась пятиоптикой, развивавшейся в работах Г. Вейля, Калуза и Ю. Б. Руммером в Советском Союзе. Изложенная выше связь между группами с инвариантами и геометриями, устанавливающая изоморфизм между различными геометриями и различными физиками, была продемонстрирована всей совокупностью работ Г. Крона. Физическая интерпретация понятия “тензор”, принадлежащая Г. Крону, к сожалению, не была должным образом оценена математиками.

Теперь, рассматривая обобщенное движение как группу преобразований с инвариантом той или иной физической величины, можно рассматривать все технические системы как группы с теми же инвариантами. Общая теория систем и общая теория групп преобразований с инвариантами тех или иных физических величин представляют собой лишь различные названия для одного и того же предмета исследования и конструирования.

Обратим внимание на физический смысл понятия “инвариант” в обыденной жизни. Оно выражает некоторое значение чего-то неизменяющегося, т. е. сохраняющегося. Неизменяющееся и сохраняющееся в обыденной жизни принято называть существующим, а иногда сущностью. Выразить сущность того или иного явления природы – значит найти нечто, что сохраняется в глубине наблюдаемой смены явлений. Однако эти сущности могут быть различных порядков: то, что является сущностью относительно одних явлений может оказаться само явлением, но относительно сущности более глубокого порядка. Подобная связь существует и между инвариантными физическими величинами. Чем дальше мы удаляемся от центра таблицы физических величин, тем более глубокие сущности мы привлекаем к рассмотрению.

Рассмотрим простой пример. Сущностью технических транспортных средств (паровоза, автомобиля, парохода, самолета, трубопровода и т. п.) можно считать функцию транспортировки грузов (измеряемых весом) с определенной скоростью в пространстве. Выделив транспортируемые с заданной скоростью грузы как “цель” системы транспортировки грузов, мы отделяем целевое назначение системы от технических средств, которые созданы конструкторами для решения указанной задачи. Произведение веса транспортируемых грузов на мгновенную скорость их транспортировки образует понятие мощность транспортной системы. Фиксируя мощность транспортной системы как цель конструирования, как заданный инвариант, все возможные технические решения по созданию транспортной системы с заданной величиной мощности можно рассматривать как варианты технического решения или как проекцию этого инварианта в одну из допустимых систем координат частного технического решения. Рассмотрим другой простой пример. Нас не устраивает существующая транспортная система, и мы хотим увеличить мощность транспортной системы на заданную величину в заданное время. Это будет уже другая система: она характеризуется ростом мощности за заданное время. Темп роста величины мощности относится уже к другой клетке таблицы физических величин, т. е. является инвариантом уже другой физической величины. При анализе систем управления реальных транспортных систем это различие является существенным: в реальных транспортных министерствах эти две различные системы соединены и их выделение в качестве подсистем общей системы управления, опирается на различие физической природы инвариантов, проявляющееся в различии целей управления этими подсистемами. Первую подсистему мы называем системой “поддержания” мощности, а вторую – системой “роста”. Если мы имеем дело с высшими производными, то их удобно выделять в подсистему “РАЗВИТИЯ”, которая должна быть найдена и опознана.

За более подробным изложением подхода ко всем системам как системам транспортировки тех или иных величин мы отсылаем читателя к ранее опубликованным работам [18-20 , 28]. Заметим, что можно говорить о системах транспорта мощности и о системах транспорта информации, имея в виду, что транспорт может осуществляться не только в пространстве, но и во времени. В этом случае принято говорить о хранении соответственно, грузов, энергии (мощности) или информации. Более детальный разбор этих систем приводит к системе транспорта величин из таблицы. Интересно отметить, что инварианты некоторых реальных систем оказались в клетках, которые весьма удалены от центра таблицы. Обычный понятийный аппарат физики не затрагивает этих инвариантов, что порождает ограниченные физикалистские подходы.

Рост возможностей общества реализуется через рост и развитие различных систем транспортировки. Этот рост обеспечивается научно-техническими идеями, источником которых был и остается человек. Полное использование всех идей, появившихся в сознании каждого отдельного человека, для роста возможностей общества и использование растущих возможностей общества для формирования человека – творца новых идей – соответствует высшему типу общественного устройства – коммунистическому обществу.

Разработка теории такого общественного устройства и является предметом научного коммунизма. Совершенно очевидно, что создание такой теории и ее превращение в действительность требует интеграции всех научных знаний, накопленных предшествующей историей человечества. Нетрудно видеть, что разработка теории научного коммунизма и разработка комплекса машинных систем для проектирования будущего – лишь два названия для одной и той же комплексной научной программы. Только в рамках комплексной научной программы можно разрешить основное противоречие между знаниями одного лица и знаниями, которые накоплены всей предшествующей историей человечества. Гегель был последним философом, который пытался создать теорию мира в целом. Создание такой теории невозможно для одного, отдельно взятого человека, но оно возможно для человечества в целом на протяжении всей прошедшей и будущей истории. Мы были вынуждены напомнить об этом результате, так как и сегодня находятся люди, которые в науке претендуют на папскую непогрешимость.

Проблема искусственного интеллекта и проблема коллективного разума требуют своего решения. Они требовали своего решения еще вчера. Не пора ли приступить к работе?

“ПРИМИТИВНЫЕ СИСТЕМЫ” И “ОБОБЩАЮЩИЕ ПОСТУЛАТЫ” Г. КРОНА

Всякую пустячную задачу или проблему можно превратить в “сверхсложную”. Это делается сравнительно легко. Обратная задача, как всегда, решается труднее. Можно ли сложные вещи сделать проще? И да, и нет. Да – потому что путь к пониманию может быть короче. Нет – потому что самый короткий путь все-таки требует времени. Путь становится короче, если школьник уже на уровне школьной программы касается переднего края науки. Можно таблицу физических величин и законов природы Р. О. ди Бартини объяснить школьнику? Вероятно, можно. Но в этом случае мы уже со школьной скамьи будем готовить специалиста по проектированию систем, специалиста по конструированию. Японская ассоциация прикладной геометрии провела уникальную работу, ориентированную на улучшение математической подготовки инженера-конструктора. И не случайно, что ассоциация использовала в качестве общей базы для всех инженеров то направление тензорного анализа, которое основал Г. Крон. Случайным является факт, что японские ученые не смогли преодолеть трудности, которые порождены нецелочисленными степенями системы основных физических величин [L], [М], [Т]. Установление изоморфизма между понятиями геометрии и понятиями физики еще не закончилось. Тем не менее, понятие ТЕНЗОР в физике как понятие ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ, которая не зависит от выбора системы координат, сохранится.

Особое место среди тензоров, каждый из которых может быть отождествлен с той или иной физической величиной таблицы Р. О. ди Бартини, занимает тензор соединения или тензор преобразования. Формально – это тензор, который имеет один штрихованный индекс, а другой индекс нештрихованный. Это означает, что тензор является посредником между двумя системами координат. Любой инженер и любой физик знает, что систем координат как физических явлений в природе нет: системы координат вводит исследователь, когда желает описать природное явление математически. Таким образом, оказывается, что тензор соединения представляет собой соединение двух точек зрения на один и тот же неизменный объект реального мира. Точки зрения на объекты реального мира всегда принадлежат отдельным людям, каждый из которых может выбирать свою точку зрения. Более того, нахождение тензора преобразования, который связывает две точки зрения на один и тот же объект реальности, свидетельствует о том, что два исследователя достигли взаимопонимания. Является ли взаимопонимание двух не исcледователей фактом физической реальности? Мы отвечаем на этот вопрос положительно. До сих пор физические теории игнорировали в описании физической реальности сам факт существования человеческого сознания, отказывая собственному мышлению физика в существовании. Но ни один из физиков не сомневается в собственном существовании. Более того, он не сомневается в том, что обладает мышлением. Но как записать собственные мысли физическим языком? Это не праздный вопрос. Мы хотим уметь отличать НАШИ МЫСЛИ о физической реальности, которые еще далеко не адекватны ей, от самой физической реальности вне нашего сознания. Оказывается, что понятиям в индивидуальном мышлении человека и соответствуют группы преобразований. Эту же мысль можно выразить иначе; каждому понятию в индивидуальном мышлении соответствует группа преобразований. Проблема распознавания образов, процесс формирования ПОНЯТИЙ и есть процесс формирования группы преобразований. Инвариант этой труппы преобразований и называла классическая философия термином сущность, а проекции этой сущности в частную точку зрения исследователя – явлением.

Тензорный анализ и создавался как инструмент описания закономерностей физического мира, позволяющий отличать физическую реальность от случайной точки зрения, зависящей от выбора той или иной системы координат. Теперь, когда объекты реальности нашли свое место в таблице физических величин, мы получили возможность корректно отделять субъективную точку зрения исследователя от самих объектов реальности. Это субъективность точки зрения и демонстрируется тензором преобразования как понятием.

Мы дали это разъяснение потому, что когда Г.Крон отождествил понятие т е н з о р с физической величиной, то тензор преобразования (по определению) выпал из этого нового определения. Теперь мы видим, что это важное и нужное понятие, которое имеет самое непосредственное отношение к проблеме искусственного интеллекта.

Основная часть наших собственных работ по синтезу логических теорий в рамках комплексных научных программ выполнена до знакомства с работами Г. Крона. Это знакомство дало нам возможность выделить то общее, что приводит к одинаковым следствиям. Поскольку личные интересы автора ориентированы на выяснение термодинамических особенностей всей совокупности явлений жизни, пришлось искать такое расширение понятий физики, которое бы включало явления жизни в физическую теорию. Классическая термодинамика не включает в теорию понятие “время”, а оно существенно для эволюции. Включение понятия “время” в термодинамику приводит к производным по времени от понятий термодинамики. Так мы переходим от понятия “свободная энергия” к понятию “поток свободной энергии”.

Работая с понятием “поток свободной энергии”, мы можем рассматривать три класса физических систем: с уменьшением потока свободной энергии, с сохранением потока свободной энергии и с ростом потока свободной энергии.

В системах с сохранением потока свободной энергии, являющихся открытыми, входящий поток энергии равен выходящему потоку свободной энергии. Теория этого класса термодинамических систем и была первой, основополагающей работой Г. Крона в 1930 г. [23]. Фактически эта теория утверждает инвариантность потока энергии или инвариантность мощности. Постулат об инвариантности мощности не может быть обоснован никакой логической теорией. Он говорит о свойствах некоторых систем физической реальности. Этот постулат не доказывается, а принимается как свойство природы, если существуют явления природы, которые не противоречат введенному постулату. Развитая Г. Кроном теория таких систем оказалась теорией сохранения или существования живых систем. В экономических явлениях инвариантности мощности соответствует режим простого воспроизводства.

Рассматривая системы с ростом потока свободной энергии, мы можем рассмотреть закон движения таких систем, разлагая величину мощности в ряд по возрастающим степеням времени (или в ряд Тейлора, как это сделано в работе Б. Г. Кузнецова). В этом разложении в ряд полной мощности, представленной частными мощностями выпуска отдельных продуктов, мы получим линейное приближение, соответствующее линейным экономическим моделям. Следующее приближение будет описываться 3-матрицей 2-сети, следующее за ним – 4-матрицей 3-сети и так далее до полиэдральных сетей.

Последовательность шагов формирования теории электромагнитных явлений в электрических сетях, начинающаяся с 1-сетей “Тензорного анализа сетей”, 2-сетей, рассмотренных Г. Кроном в “Неримановой динамике вращающихся электрических машин” [24], и до полиэдральных сетей диакоптики образует стальной каркас, направляющий движение к созданию искусственного интеллекта. Работы Г. Крона логичны и понятны, если следить за его логикой с первых до последних работ. Они требуют некоторой подготовки читателя, о которой и говорил Г. Крон [11]: Необходимая подготовка читателя. Разумеется, всего, что встречается в жизни, не предусмотришь. Если читатель, оказавшись перед трудной задачей, которую он не может решить, в отчаянии воскликнет: “Попробую я применить диакоптику и посмотрю, действительно ли она может то, на что претендует”, – он получит один из основных жизненных уроков. Он обнаружит, что прежде чем он смог бегать, ему необходимо было научиться ходить, что прежде чем он смог ходить, он должен был научиться ползать. Инженер должен сначала решать методом расчленений простейшие задачи, чтобы понять, что диакоптика дает. Затем постепенно он должен прокладывать свою дорогу, чтобы достигнуть той цели, которую он поставил перед собой. Прежде чем применять диакоптику к исследованию переходных процессов, инженер должен научиться использовать ее в исследовании установившихся процессов. Прежде чем он попытается решать по частям задачи о колебаниях, он должен приобрести опыт в решении по частям численных задач.

ЗАКЛЮЧЕНИЕ

Мы не призываем читателя немедленно приступить к разработке комплекса машинных систем, реализующего функцию оперативной памяти человечества. Мы полагаем, что знакомство с этой важной и нужной областью поможет ему в решении конкретных проблем, которые он решает сегодня.

Мы хотели показать, что на каждую научную проблему могут существовать самые различные точки зрения. Одной из возможных и важных точек зрения на проблему искусственного интеллекта является точка зрения автора книги – Е. А. Александрова. В ней уделено больше внимания не физическому, а математическому подобию. Известны и другие подходы к проблеме искусственного интеллекта. В настоящее время еще нет полной сводки различных подходов, и публикуемая книга найдет свое место среди них.

Я лично считаю, что все направления так или иначе будут концентрироваться вокруг подхода Г. Крона и подхода японской ассоциации прикладной геометрии. Однако это, возможно, заблуждение. К сожалению, отмеченные мною научные направления пока недостаточно известны в нашей стране, а редакторы предшествующих изданий Г. Крона своей “снисходительной” позицией к “неразумному мальчику”, который не понимает элементарных вещей, не способствовали лучшему знакомству с инженером-физиком № 1. Способствовать знакомству с этой областью будет перевод “Тензорного анализа сетей”, который готовится издательством “Советское радио”. Не исключено, что будут предприняты усилия по ознакомлению широких кругов инженеров с работами японской ассоциации прикладной геометрии, возглавляемой проф. К. Кондо. Наши электротехники обеспечили перевод книги П. Димо “Узловой анализ электрических систем” (М., “Мир”, 1973) (более точное название “Узловой анализ энергетических сетей”), в которой работы Г. Крона уже называются “классическими”. Готовятся переводы книг Хэппа “Диакоптика и сети” и Брамеллера с соавторами “Практическая диакоптика”. Несколько в стороне от этого направления, но образуя существенную часть решения проблемы, стоят работы по системному анализу С. Оптнера [26] и С. Янга [27], снабженные прекрасными предисловиями С. П. Никанорова.

Я хочу выразить свою признательность академику В. В. Парину, который с 1948 г. определил мой интерес к проблеме жизни, и моим друзьям – Р. О. ди Бартини, Г. П. Мельникову, С. П. Никанорову и Г. Н. Поварову, которые резко сократили число моих научных промахов.

СПИСОК ЛИТЕРАТУРЫ

1. Эшби У. Р. Схема усилителя мыслительных способностей. В кн.: Автоматы, М., ИЛ, 1956, с. 281–305.
2. Кузнецов Б. Г. Физика и экономика, М., “Наука”, 1967.
3. Казначеев В. П., Кузнецов П. Г. О некоторых вопросах теоретической биологии. – В кн.: Вопросы патогенеза и терапии органосклерозов, Новосибирск, 1967.
4. Kusnetzow P. G. Sputnik-Scalar. Technische Gemeinschaft 1970, № 3, р. 26–32.
5. Афанасьев В. Г., Чесноков В. С. – В сб.: Научное управление Обществом, вып. 6. М., “Мысль”, 1972, с. 268–331.
6. Система “Спутник 1”. Методики и методические материалы. ЦЭМИ АН СССР. М., МГПИ им. В. И. Ленина, .1968.
7. Ньюэлл А., Шоу Дж., Саймон Г. Эмпирические исследования машины “логик-теоретик”; пример изучения эвристик. – В кн.: Вычислительные машины и мышление. М., “Мир”, 1967, с. 113–114.
8. Миллер Дж., Галантер Е., Прибрам К. Планы и структура поведения. М., ИЛ, 1964.
9. Евреинов Э. В., Косарев Ю. Г. Однородные универсальные вычислительные системы высокой производительности. Новосибирск, “Наука”, 1966.
10. Kron G. Tensor Analysis of Networks. N. Y., 1939.
11. Крон Г. Исследование сложных систем по частям-диакоптика. М., “Наука”, 1972.
12. Memoirs of the Unifying Study of Basic problems in engineering sciences by means of geometry. 1955, v. 1; 1958, v. 2.
13. Бартини ди Р. О. ДАН СССР, 163, № 4, 1965.
14. Бартини ди Р. О. Соотношения между физическими величинами. – В сб.: Проблемы теории гравитации и элементарных частиц. М., Атомиздат, 1966, с. 249–266.
15. Мышкис А. Д. Математика. Специальные курсы. Для втузов. М., “Наука”, 1971.
16. Саймон Г. Науки об искусственном. М., “Мир”, 1972.
17. Беш Г. География мирового хозяйства. М., “Прогресс”, 1966.
18. Odum H. T. Environment. Power and Society, N.Y., 1971.
19. Подолинский С. А. Труд человека и его отношение к распределению энергии. Журнал “Слово”, № 4–5, 1880, с. 135–211.
20. Кузнецов П. Г. О возможности энергетического анализа основ организации общественного производства. – В сб.: Эффективность научно-технического творчества. М., “Наука”, 1968, с. 133–162.
21. Кузнецов П. Г. Термодинамические аспекты труда, как отношения человека к природе. – В сб.: Природа и общество. М., “Наука”, 1968, с. 298–311.
22. Афанасьев В. Г., Кузнецов П. Г. Некоторые вопросы управления научно-техническим прогрессом. – В сб.: Научное управление обществом. М., “Мысль”, 1970, вып. 4, с.211-231.
23. Kron G. Generalised theory of electrical machinery. – AIEE Trans. 1930, v. 49, № 4, p. 666-685.
24. Kron G. Non-Riemanmian dynamica of rotating electrical machinery. – MIT, 1934, v. 13, № 2, p. 103-194.
25. Boulding K. E. The image. Ann Arbor, Univ, of Michigan press., 1956.
26. Оптнер С. Системный анализ для решения деловых промышленных проблем. М., “Сов. радио”, 1969.
27. Янг С. Системное управление организацией. М., “Сов. радио”, 1972.
28. Бартини Р. О., Кузнецов П. Г. Множественность геометрий и множественность физик. – В сб.: “Моделирование динамических систем”. Брянск, 1974, с. 18-29.

 

Выходные данные статьи: Кузнецов П. Г. Искусственный интеллект и разум человеческой популяции. – В кн.: Александров Е. А. Основы теории эвристических решений. – М., 1975.