---

Г. Крон

Тензорный анализ сетей.

ГЕОМЕТРИЧЕСКИЕ ИНТЕРПРЕТАЦИИ
1. ГЕОМЕТРИЧЕСКИЙ ЯЗЫК

I. Большинство наук имеет дело с явлениями, которые можно описать системами уравнений. Давно было замечено, что когда казалось бы не связанные друг с другом явления описываются в терминах фундаментальных понятий, то уравнения их имеют один и тот же вид. Например, многие уравнения гидродинамики, теории упругости, электродинамики и дифференциальной геометрии имеют одинаковый вид несмотря на то, что различные члены в этих уравнениях представляют разные понятия в разных науках.

В течение последнего столетия появилась тенденция вводить универсальный язык, на котором подобные уравнения различного происхождения интерпретируются и представляются наглядно на общей основе. Таким языком является геометрия. Следовательно, чтобы сказать: система уравнений описывает поведение электрической машины или гироскопа, или движущегося электрона, – на языке геометрии говорится, что система уравнений описывает определенную геометрическую кривую в n-мерном пространстве или движение частицы по этой кривой. Свойства различных типов кривых, поверхностей и пространств всегда соответствуют некоторым свойствам исследуемой частной физической системы. Например, сингулярность на поверхности соответствует наличию электрического заряда; кривизна пространства в точке является показателем динамической устойчивости или неустойчивости осциллирующей динамической системы.

Таким образом, если уравнения различных наук выражены нa геометрическом языке, то все результаты этих наук можно объединить в один общий фонд и применять в других науках, не развивая каждый раз ту же теорию заново, но на другом языке.

II. Вообще говоря, ситуация для получения унифицированной точки зрения в технике значительно менее благоприятна, чем в фундаментальных науках. После развития в условиях изоляции в течение нескольких десятилетий эти дополнительные технические знания настолько удалились от своих “родителей” – фундаментальных наук, что новый запас знаний стал закрытой книгой для всех, кроме специалистов, посвятивших ему жизнь, но потерявших из-за этого всякий контакт с фундаментальной наукой. Теория сетей и вращающихся электрических машин является классическим примером такого роста технических знаний в условиях изоляции со всеми присущими ему неудобствами, такими как необходимость различных теорий для каждой машины.

Цель данной книги – переформулировать имеющиеся знания в области электрических сетей в терминах фундаментальных инвариантных понятий, используемых в современной электродинамике и геометрии, чтобы упростить их понимание и открыть новые каналы исследования их анализа и синтеза, следуя возможно ближе путям развития фундаментальных наук. Всегда выявляется, что геометрическая формулировка технических задач много проще, короче и элегантнее, чем способ, которым привыкли их выражать специалисты по электротехнике; геометрическая формулировка дает лучшее и более ясное наглядное представление. Известно также, что большинство наиболее современных математических инструментов, подобных тензорному анализу, являются более простыми для понимания, более удобными для применения к сложным проблемам и быстрее приводят к численному результату, чем элементарные средства, развитые наудачу под давлением случайной необходимости.

III. В этой главе некоторые ранее введенные физические понятия и аналитические процессы проиллюстрированы геометрическим языком. Содержание главы не является необходимым для понимания последующих глав. Однако каждый желающий читать другие учебники по тензорному анализу должен быть хорошо знаком с содержанием этой главы, поскольку практически все книги по тензорному анализу используют геометрический язык.

Некоторые части главы представляют собой утверждения, доказательства которых приводятся в книгах по тензорному анализу. Здесь не делается попытка дать точные определения.

2. ГЕОМЕТРИЗАЦИЯ ФИЗИЧЕСКИХ ПРОБЛЕМ

I. Переход от физической проблемы к геометрической интерпретации осуществляется с помощью следующего допущения: “Система n уравнений с n переменными (с временем в качестве параметра) может представлять либо поведение динамической системы с n степенями свободы, либо движение точки по кривой, расположенной в n-мерном гипотетическом пространстве и записанной в некоторой частной системе координат”.

II. Например, пусть даны две катушки, в которых уравнение напряжения e_α = z_αβi^β имеет вид

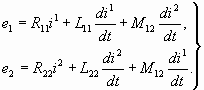(8.1)

Пусть величины этих токов в двух катушках в определенный момент времени будут i¹ = 1,5 А и i² = 1,765 А. В следующий момент пусть эти токи будут i′ = 0,87 А и i² = 1,49 А. Еще позднее i¹ = 0,763 и i² = 1,175 и еще позднее i¹ = l,105 и i² = 0,235 и т. д.

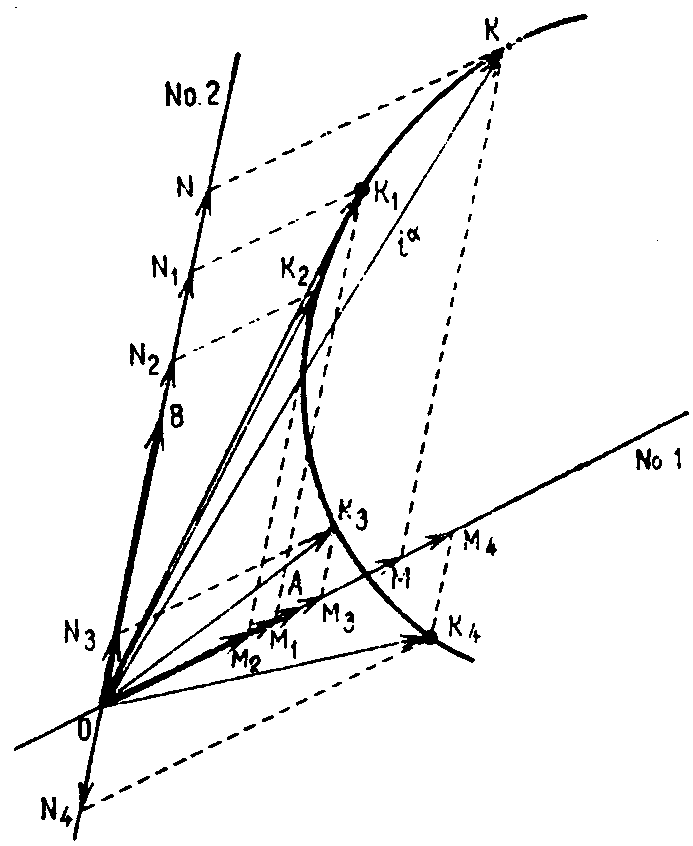
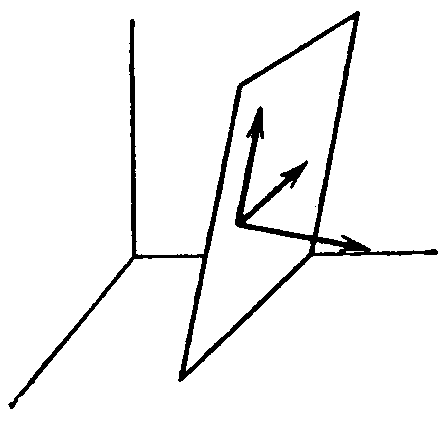
Чтобы представить изменение токов как геометрическую задачу, допустим сначала, что гипотетическое пространство, которое должно быть введено, является хорошо знакомым “линейным” пространством, в котором оси координат – прямые линии, расположенные под произвольным углом друг к другу. Если обнаружено, что характеристики этого пространства недостаточны для объяснения этапов, действительно выполняемых при изучении сетей, то это пространство можно модифицировать или заменить другим, которое точнее соответствует действительным шагам. Следовательно, пусть в качестве первого приближения даны две пересекающиеся линии, называемые “координатными осями”, или системой координат, расположенные под произвольным углом друг к другу (рис. 8.1.), и пусть вдоль них выбраны два произвольных отрезка ОА и ОВ,

Рис. 8.1. Представление контравариантного вектора iα в прямолинейной системе координат.

длина которых принята за “единицу”, представляющую 1 А. Пусть величина тока в катушке 1 отложена по линии 1 в единицах ОА, а величина тока в катушке 2 – по линии 2 в единицах ОВ. Соединим две точки, которые измеряют ток в каждый момент времени, вычертив параллелограмм, подобный ОМКN, где проекции точки К представляют два тока i¹ = ОМ = 1,5 и i² = ON = 1,765 в некоторый момент времени. С течением времени точка К описывает кривую КК₁К₂К₃К₄…, называемую “траекторией”. Компоненты точки К, вдоль координатных осей дают мгновенные значения токов, текущих в двух катушках. Последовательные изменения токов в двух катушках образуют траекторию, описываемую точкой К.

Плоскость, в которой движется точка К, называется “линейным” или “аффинным” пространством.

III. Если имеются три катушки, то в качестве координатной системы можно выбрать три взаимно пересекающиеся линии, расположенные в пространстве, а не на плоскости, последовательные изменения токов в трех катушках опять будут описываться движением точки К.

Если имеется более трех катушек, то, используя тот же “оборот речи”, опять говорят, что точка К, движется в n-мерном аффинном пространстве и компоненты этой точки по n взаимно пересекающимся осям представляют в каждый момент времени мгновенные значения токов, протекающих в n катушках. Нужно заметить, что не следует делать каких-либо попыток наглядного представления n-мерного пространства.

3. ПРЕДСТАВЛЕНИЕ КОНТРАВАРИАНТНОГО ВЕКТОРА

I. Линию, соединяющую движущуюся точку К с началом координат О, называют “контравариантным вектором” и говорят, что в n катушках протекает только один ток, представленный вектором OK, называемым “вектором тока”, и что компоненты этого вектора по осям координат представляют индивидуальные токи, протекающие в катушках.

II. Возникает вопрос: если компоненты вектора ОК – это действительно существующие токи, протекающие в катушках, то чему соответствует сам вектор ОК в физической системе?

Ответ состоит в том, что сам вектор ОК в физической системе ничему не соответствует. Вектор ОК является понятием, изобретенным для того, чтобы существовало что-то, имеющее компоненты. Таким образом, “вектор” является функцией; его компоненты, однако, измеряемые физические величины.

Векторы, которые здесь используются, существенно отличаются от обычных векторов, используемых инженерами. Векторы, используемые инженерами, такие как “скорость” тела, физически существуют, а их компоненты являются фикцией, тогда как используемые в книге векторы являются фикцией (по крайней мере до сих пор), а их компоненты физически существуют.

Иначе говоря, векторы, которые описывают явления, имеющие место в реальном трехмерном мире наших ощущений, отличны от векторов, изобретенных для описания явлений, для которых реальное физическое пространство является чуждой характеристикой.

III. Поскольку вектор ОК ничему не соответствует в частной физической системе, то нет смысла говорить о его “величине” или “направлении”; его “компоненты” представляют токи в катушках, но “величина” и “направление” вектора ОК еще не определены геометрически.

В гл. 18 показано, как можно приписать вектору ОК некоторую физическую интерпретацию, а значит, приписать численные значения тому, что называется “величина” и “направление” вектора ОК. Однако эти понятия имеют мало общего с “величиной” и “направлением” в их обычном значении. Они принимают обычный смысл только в частном случае, когда оси координат взаимно перпендикулярны, а единичные векторы осей имеют одинаковую длину. В неподвижных сетях такая ситуация встречается лишь в тривиальном случае, когда катушки: 1) эквивалентны, 2) имеют единичную собственную индуктивность, 3) не имеют взаимных индуктивностей. Только в этом случае можно сказать, что точка К движется в n-мерном обычном (евклидовом) пространстве и вектор имеет “величину √i₁² + i₂² + i₃² + ..., представляющую квадратный корень из удвоенной “запасенной магнитной энергии” системы.

Ещё раз подчеркнем, что в общем случае векторы не имеют ни “величины”, ни “направления”. Вектор имеет только “компоненты”, которые действительно существуют. Он определяется как множество величин, формула преобразования которых содержит или С_α´^α, или обратную С_α^α´.

4. НЕДОСТАТОЧНОСТЬ ОБЫЧНЫХ ПРОСТРАНСТВ

I. Может возникнуть вопрос, почему в качестве системы координат выбраны линии, пересекающиеся под произвольным углом, и почему в качестве одного ампера в каждой катушке выбраны два отрезка неравной длины. Более логично было бы выбрать две (или

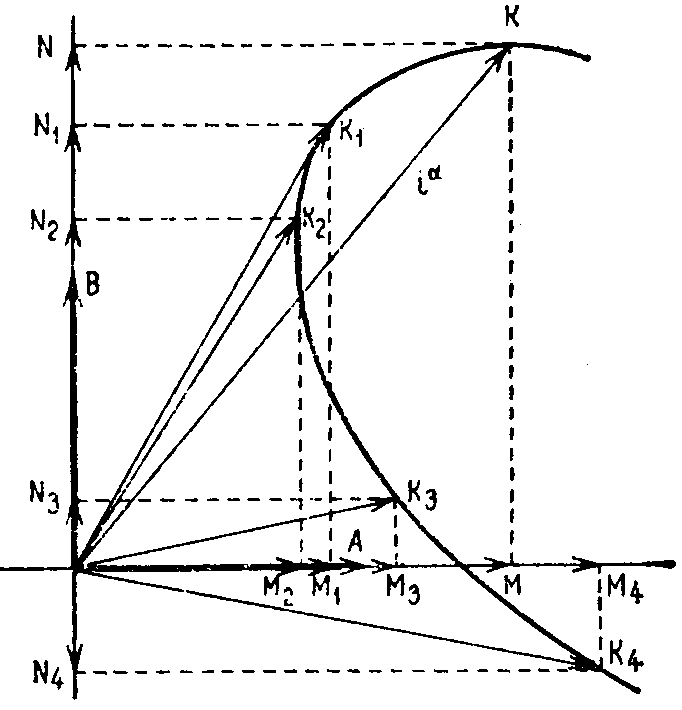
Рис. 8.2. Прямоугольная система координат.

больше) линии, пересекающиеся под прямым углом (рис. 8.2.), и два (или более) равных вектора в качестве единичных векторов. В этом случае легче изобразить и интерпретировать движение точки, поскольку пространство является обычным евклидовым пространством. Существуют две причины введения прямолинейной (и не прямоугольной) системы координат и неравных единичных векторов. Первой причиной недостаточности обычного пространства является то, что выбранное представление должно быть справедливо для произвольных систем координат. Если вектор тока ОК представляется только в прямоугольной системе с равными единичными векторами, то разрешенными преобразованиями могут быть только вращения (и переносы), для которых детерминант тензора преобразования С всегда равен единице. Однако

тензоры преобразования, используемые в исследованиях сетей, являются гораздо более сложными; это значит, что системы координат и единичные векторы должны быть более разнообразны.

Вторая причина состоит в том, что в дополнение к геометрической интерпретации токов и напряжений в дальнейшем предполагается нахождение геометрической интерпретации и других электромагнитных величин. Например, если предполагается интерпретировать величину вектора тока ОК как величину, которая в каждый момент пропорциональна запасенной магнитной энергии l_αβi^αi^β, то обнаруживается, что различные оси должны располагаться под разными углами и единичные векторы должны быть неравными; это неравенство углов и величин единичных векторов является функцией от собственных и взаимных индуктивностей. Другой пример: если предполагается представить геометрически электрические разряды, имеющиеся в обмотках вращающейся электрической машины, то нельзя предполагать, что оси координат располагаются в “плоском пространстве”, подобном плоскости; они должны располагаться в n-мерном искривленном пространстве, подобном сферической поверхности (в одномерном случае), а сами координаты оси должны быть кривыми линиями. По мере того как все большее и большее число электромагнитных величин требуется интерпретировать геометрически, все пространства и конфигурации, расположенные в них, становятся соответственно все более сложными.

II. В тех случаях, когда не предполагается вводить группы новых координатных систем для представления новых систем или новых точек зрения, а также не предполагается позднее вводить геометрическую интерпретацию других величин, кроме выбранных переменных, выбор прямоугольной системы координат и равных единичных векторов в любой физической проблеме независимо от сложности является совершенно правильным. Таким представлением, например, является поверхность давление – объем – температура (р–v–Т), показывающая графически уравнение состояния термодинамической системы. Однако на таких диаграммах понятия “расстояние между двумя точками” или “угол между двумя линиями” и другие не имеют эквивалентов в физической системе.

Геометрическое представление любой физической проблемы является удовлетворительным тогда и только тогда, когда:

1) оно сохраняет силу для всех координатных систем, которые должны быть введены;
2) оно представляет геометрически максимальное число физических величин, относящихся к данной проблеме, и точно показывает их взаимоотношение в любой момент времени.

III. Большее разнообразие сложных координатных систем и неевклидовых криволинейных пространств еще следует ввести в современную физику, чтобы удовлетворить этим двум требованиям корректного геометрического представления физических явлений. Это особенно необходимо для представления электромагнитных явлений, с которыми сталкиваются инженеры-электротехники; здесь требуются очень сложные типы пространства, и большая часть современного тензорного анализа и дифференциальной геометрии обязана своим развитием этим попыткам геометрического представления электромагнитных явлений. Такое представление совершенно необходимо для пояснения физической сути явлений и определения пути атаки еще не решенных проблем.

Подчеркнем, что нет необходимости иметь точное количественное соответствие физической задачи ее геометрическому представлению. Достаточно иметь качественное соответствие, т. е. предложить грубое, но еще работающее наглядное представление.

IV. По мере того как растет сложность электромагнитных явлений и координатных систем, необходимых для использования, пропорционально возрастает сложность геометрических конфигураций, которые требуется ввести, и сложность пространств, в которых эти конфигурации располагаются.

С появлением распространяющихся электромагнитных волн, движущихся проводников, ускоренное движение которых вызывается магнитным полем, геометрическое представление становится чрезвычайно сложным.

Даже представление, данное на рис. 8.1., фактически недостаточно для геометрического изображения поведения системы катушек при всех условиях. Например, если токи в каждой катушке представлены не действительными, а комплексными числами, то такие токи не могут измеряться единичными векторами по осям 1 и 2. В этом случае координатные оси считаются расположенными не в обычном пространстве, а в пространстве нового типа, называемом “унитарным”, его можно представить только математически. Следовательно, все диаграммы, все геометрические выражения, такие как “координатные оси”, “единичный вектор”, “пространство”, “плоскость”, “пересечение”, должны восприниматься инженером только как вспомогательное средство для наглядного представления математических шагов, для облегчения запоминания их особенностей. Геометрический язык должен использоваться только как “оборот речи”, а не как точное описание уравнения поведения.

V. Следует подчеркнуть, что n-матрицу нельзя представить геометрически. Чтобы представить математически посредством n-матрицы геометрическую сущность, такую как линия, плоскость или эллипсоид, рассматриваемую в некоторой системе координат, необходимо, чтобы та же самая сущность могла быть представлена посредством другой n-матрицы в другой системе координат. Другими словами, геометрическая сущность представляется целой последовательностью n-матриц, а не одной n-матрицей, ибо каждая n-матрица представляет компоненты геометрического объекта только в частной системе координат.

Такая последовательность n-матриц называется здесь “геометрическим объектом”, а именно n-матрица с закрепленной формулой преобразования, которая позволяет геометрическому объекту принимать ряд значений, каждое из которых представляется n-матрицей. Таким образом, как с геометрической сущностью, так и с “геометрическим объектом” связывается большое, обычно бесконечное, количество n-матриц, по одной для каждой системы координат.

Следовательно, каждая геометрическая сущность (линия, плоскость и т. д.) представляется “геометрическим объектом”, а не просто n-матрицей.

5. ПРЕДСТАВЛЕНИЕ КОВАРИАНТНОГО ВЕКТОРА

В предыдущих параграфах было показано, что имеется два типа векторов (контравариантные и ковариантные), причем каждый из них при изменении системы

Рис. 8.3. Представление ковариантного вектора еα.

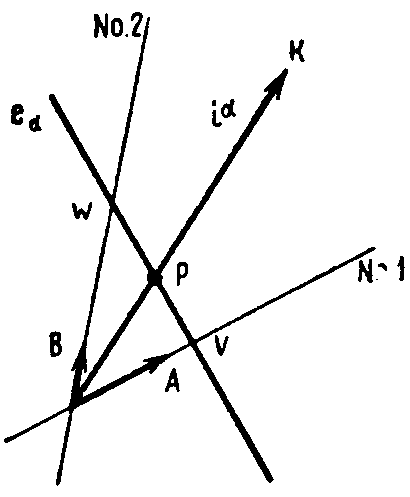
координат имеет свою формулу, преобразования. Из-за этого различия в формуле преобразования обнаружено, что ковариантный вектор нельзя представить геометрически, как контравариантный вектор, т. е. точкой в пространстве. Пусть снова система координат задана своими единичными векторами (рис. 8.3.) и мгновенное значение приложенного напряжения в двух катушках равно 0,8 и 0,25 В, т. е. Для представления этих компонент по оси 1 измеряют обратную 0,8 величину, т. е. 1,25 единиц V, а по оси 2 обратную 0,25 величину, а именно 4 единицы W. Линия, проходящая через точки V и W, представляет ковариантный вектор еα..

В общем случае в n-мерном пространстве “ковариантный вектор” е_α, имеющий n компонент, представляется (n-1)-мерной гиперплоскостью. “Компоненты” вектора е_α являются обратной величиной отрезков, отсекаемых плоскостью от координатных осей. При изменении приложенных напряжений от момента к моменту отрезки изменяются, и плоскость движется из одной части пространства в другую.

Если i^α используется в качестве переменной, то уравнение плоскости (представляемой e_α) есть

eα iα = 1

(8.3.)

или 0,8i^α + 0,25i^b = 1. Например, если i^b = 0, то i^α = 1/0,8 = 1,25 = OV.

6. ПРЕОБРАЗОВАНИЕ СИСТЕМЫ КООРДИНАТ

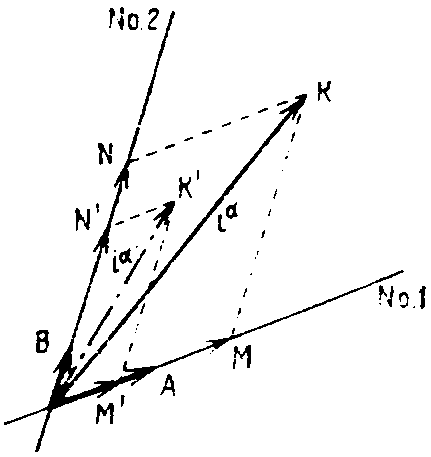
Пусть вместо линий 1 и 2 в качестве координатных осей введена другая система линий 1΄ и 2´ (рис. 8.4.). Вдоль этих новых осей пусть снова отложены два произвольных вектора ОА΄ и ОВ΄, которые названы “единичными”.

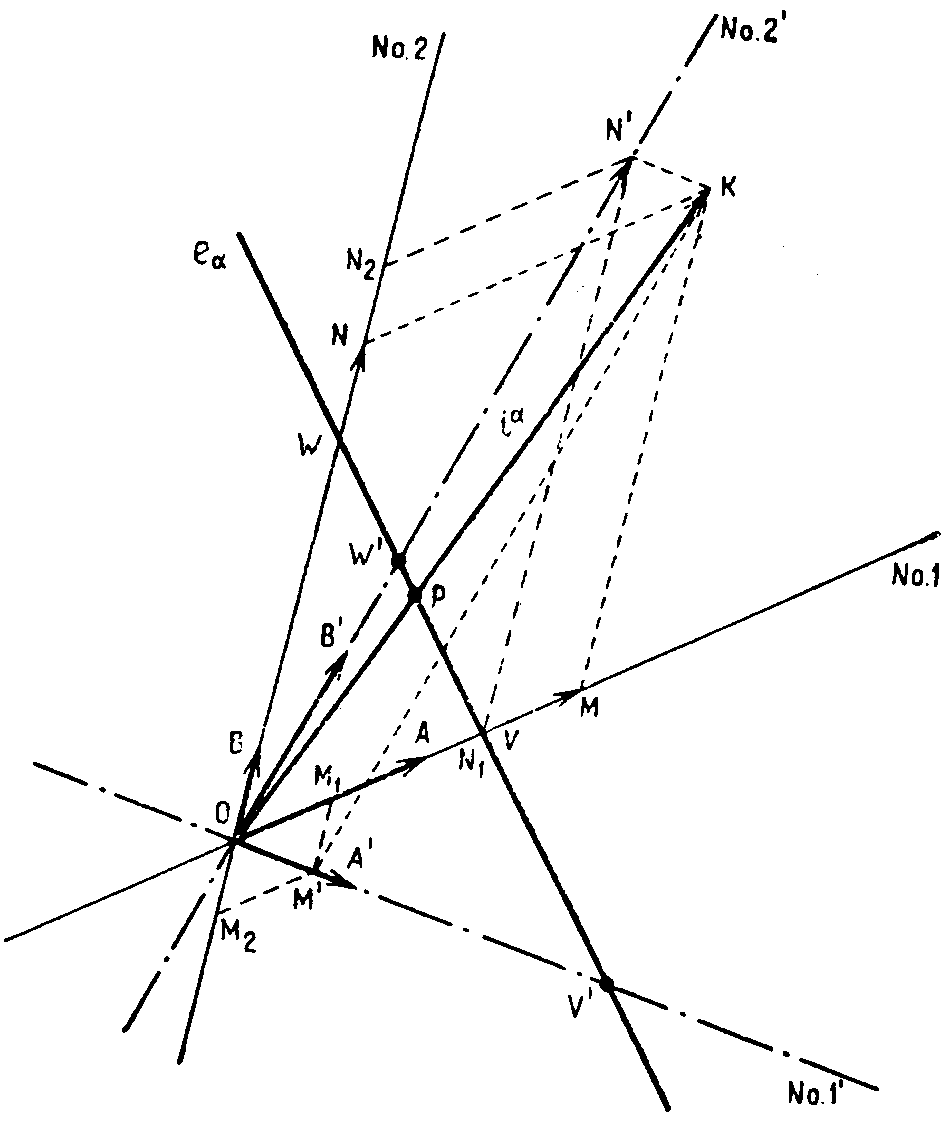
Рис. 8.4. Преобразование системы координат.

(Можно считать, что фиксированные индексы 1, 2 или а, b, появляющиеся вдоль n-матриц, и представляют эти единичные векторы).

В этих новых осях компонентами контравариантного вектора i^α = OK является OM΄ = 0,635 и ON΄ = 3,46, измеряемые в терминах, заданных вектором OА΄ и OВ΄ соответственно. Таким образом, компонентами i^α в старых и новых координатных осях являются

Для того чтобы найти тензор преобразования С = С_α^α΄, нужно установить соотношение между старыми компонентами ОМ, ON и новыми компонентами ОМ΄ θ ON΄i^α в виде i = С х i΄. Следовательно, ОМ и ON должны быть выражены через ОМ' и ON'.

Проводя из точек М' и N' линии, параллельные старым осям, можно выразить ОМ и ON через проекции ОМ' и ON' на старые оси в виде

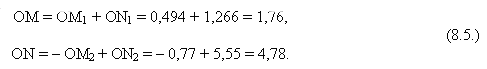
Выражая проекции в виде OM΄ и ON΄ (где OM΄ = 0,634 и ON΄ = 3,46),

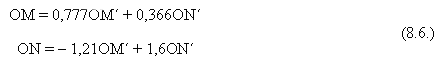
или через токи

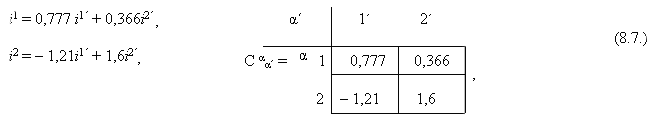
тензор преобразования определяют коэффициентами при новых компонентах тока.

Как только тензор преобразования С установлен, компоненты любого другого вектора или тензора в новых осях можно найти посредством их формулы преобразования. Компоненты ковариантного вектора e_α в новых осях e΄ = С_t х e или

e_α΄ = С^α_α΄ e_α

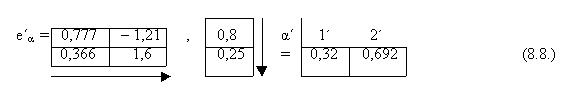
Отрезки OV΄ и OW΄, отсекаемые плоскостью e_α от новых осей (рис. 8.4.), равны 3,12 и 1,44. Обратные им величины (представляющие компоненты e_α΄) равны 0,32 и 0,692, что является подтверждением значения e_α, найденного с помощью формулы преобразования.

Нельзя не отметить, что единственным критерием того, что множество величин (таких, как токи или напряжения в катушках сети), расположенных в строку, называется величинами “компонент вектора” (и представляется точкой или (n-1)-мерной плоскостью), является то, что при переходе к новой системе координат эти величины преобразуются посредством умножения на С или обратную ей С^-1. Не существует никакого другого критерия, отличающего систему величин, называемую “компонентами вектора”. Эти векторы не имеют никаких других атрибутов; они не имеют ни “величины”, ни “направления”, ни “ориентации”.

Из того факта, что их формула преобразования содержит С или С^-1 только один раз, их компоненты располагаются в строку, а их базовая буква имеет один индекс. Если системе чисел С или С^-1 требуется дважды, то тогда и только тогда эти числа располагаются в квадрат, а их базовая буква имеет два индекса. Вполне возможно, что то же самое множество чисел можно в одной задаче расположить в строку, а в другой – в квадрат. В действительности даже в одной проблеме может случиться, что в одном типе системы координат множество чисел рассматривается как вектор и располагается в строку, а в другом типе координатной системы это же множество чисел рассматривается расположенным в квадрат. Единственным критерием способа расположения множества величин является их “формула преобразования” или “уравнение преобразования”.

7. ПРЕОБРАЗОВАНИЕ ТОЧЕК ПРОСТРАНСТВА

I. Наряду с тем, что рассматривается геометрически уравнение преобразования i^α = C^α_α΄i^α΄ или x^α = f (x^α΄) как преобразование системы координат, используется и другая точка зрения, а именно, что система координат остается неизменной, а вместо нее совершает движение к другой точке сама точка в соответствии с уравнением преобразования

iα = Cαα΄iα΄. Например, пусть iα, как показано на рис. 8.5., до преобразования представлена точкой K, с компонентами OM = 1,76 и ON = 4,28. После преобразования ее компоненты становятся ОМ' = 0,635 и ON' = 3,46; эти числа можно отложить в тех же осях, которые были до преобразования, при этом образуется новая точка К'. Вектор ОК можно теперь считать представляющим iα΄. Другими словами, результат преобразования iα = Cαα΄iα΄ заключается в движении точки К в точку К'. Взяв различные компоненты iα, можно переместить все точки пространства в новые положения. Таким образом, имеются две точки зрения на геометрическое представление преобразования iα = Cαα΄iα΄:

Рис. 8.5. Преобразование точки iα.

1) оно или преобразует систему координат и оставляет точки пространства неизменными;
2) или преобразует точки пространства и оставляет систему координат неизменной.
Эти две точки зрения эквивалентны.

II. Сколь велико изменение, вызываемое преобразованием точек пространства i^α = C^α_α΄i^α или x^α = f (x^α΄), зависит от вида C^α_α΄. Каждый тип геометрии имеет свою собственную группу C^α_α΄. В общем случае может быть установлено:

1. В евклидовой геометрии допустимы только такие C^α_α΄, которые могут любым способом переносить или вращать точки пространства без изменения формы фигур.
2. В дифференциальной геометрии допустимы только такие C^α_α΄, которые могут изгибать пространственные формы, однако без разрыва и растяжения.
3. В топологии допустимы только такие C^α_α΄, которые могут растягивать и изгибать пространство-структуру без разрывания его.
4. Однако оказывается, что преобразования C^α_α΄, встречающиеся в электротехнике, являются еще более общими, чем любые используемые в этих геометриях, поскольку они могут разрывать на части представленное пространство-структуру и преобразовывать его в другие типы пространств-структур.

III. Хотя пространства движутся, изгибаются, растягиваются или разрываются, определенные свойства, связанные с ними, остаются “инвариантными”, не зависящими от производимых изменений. Например, при изгибании поверхности угол между двумя линиями, нанесенными на поверхность, остается инвариантом, а при растягивании поверхности свойство двух линий пересекать друг друга является инвариантным свойством. Тензорный анализ является инструментом для открытия таких инвариантов.

8. ПРЕДСТАВЛЕНИЕ МОЩНОСТИ

Когда контравариантный вектор i^α и ковариантный вектор e_α, заданы уравнениями (8.2.) и (8.4.), их произведение (линейная форма)

eαiα = (0,8) х (1,76) + (0,25) х (4,78) = 2,61

(8.9.)

является скаляром, тензором нулевой валентности, представляющим мгновенную мощность, поступающую в катушки. Это число, скаляр, представлено на рис. 8.4. отношением двух длин

P = eαiα = OK/OP = 2,61,

(8.10.)

причем отрезки можно измерять в любых единицах, поскольку оба лежат на одном и том же направлении. OP является линией, отсекаемой плоскостью e_α от вектора i^α. Таким образом, произведение ковариантного вектора e_α на контравариантный i^α является скаляром, представленным отношением длины i^α и частью i^α, отсекаемой плоскостью e_α. Обе длины измеряются произвольными единицами.

Когда вводится новая система координат, это отношение остается неизменным (это очевидно, если выбрана первая точка зрения на С). Таким образом, линейная форма e_αi^α является инвариантом относительно преобразования системы координат.

9. ПРОСТРАНСТВА И КОНФИГУРАЦИИ, НАКЛАДЫВАЕМЫЕ НА НИХ

I. Если дано множество из n катушек, а также токи, протекающие в катушках, поведение системы можно представить движением точки (и других геометрических конфигураций) в n-мерном пространстве. (Представленная геометрическая картина является лишь первым приближением к точной картине, которая будет дана в последующем изложении).

Геометрическое представление физического явления, имеющего место в катушках, можно сгруппировать в два главных направления.

1. Если даны n отдельных катушек, взаимосвязанных произвольно, образуя k контуров и n–k узловых пар, но не испытывающих воздействия в виде токов и напряжений, то геометрическая ситуация представляется установлением факта: дано n-мерное пространство.

С этим пространством связываются определенные свойства, называемые его “структурой”, которые ассоциируются с конструктивными константами r_αβ, l_αβ, C^αβ и др. катушек и определяются ими. Соотношение между конструктивными константами и соответствующими “структурами” в n-мерном пространстве рассматривается в гл. 18.

2. Если в катушках существуют токи и напряжения, т. е. катушки возбуждены, то мгновенные значения токов и напряжений представляются геометрической конфигурацией, например точкой или (n–1)-мерной плоскостью, наложенной (или вложенной) в данное n-мерное пространство. С течением времени, по мере изменения мгновенных значений электрических величин представляющие их конфигурации движутся, описывая определенные кривые, называемые “путями”.

II. Следует подчеркнуть резкое различие, с одной стороны, между невозбужденной системой катушек и возбужденной, содержащей электрические конфигурации; с другой стороны, между пустым пространством и пространством, которое содержит геометрические конфигурации. В обычных электротехнических проблемах нетрудно отличить конструкционные константы материальных конфигураций от электрических величин, наблюдаемых в них. Однако по мере того как электрические явления, например в электронике, становятся все более и более неуловимыми, возникают трудности, достигающие кульминации в теории относительности, где различие между материальными конструкциями и накладываемыми электрическими величинами само собой исчезает и электрические явления представляются не как наложенными на пространство, а как “конструктивные константы” или “структура” самого пространства. Если удалить электрические величины (заряды, напряженности поля, плотность потоков и т. д.), то и само пространство исчезает.

10. ОРТОГОНАЛЬНЫЕ ПОДПРОСТРАНСТВА

Плоскость, лежащая в действительном пространстве, называется двухмерным “подпространством” трехмерного пространства. Если в пространстве выбрана система трех осей, две из которых лежат в плоскости, а третья перпендикулярна ей (рис. 8.6.), то любая точка, движущаяся в плоскости, не имеет компоненты по третьей оси.

Рис. 8.6. Двухмерное подпространство в трехмерном пространстве.

1. Если сеть из n катушек рассматривается как контурная сеть с k контурами (т. е. с k переменными токами), то движение точки ограничено только k-мерным подпространством полного n-мерного пространства сети. Компоненты, представляющие движение точки по k координатным осям, представляют k контурных токов. Компоненты, представляющие движение точки по остальным (n–k) координатным осям, равны нулю, что соответствует равенству нулю токов нагрузки, снимаемых с этих узловых пар. 2. Точно так же, если та же сеть из n катушек рассматривается как узловая сеть, имеющая n–k узловых пар (где токи и напряжения заданы только на узловых парах), то движение представляющей точки ограничено (n–k)-мерным подпространством того же n-мерного пространства, но

точки которого не включены в предыдущее k-мерное пространство. Это означает, что теперь движущаяся точка не имеет отличных от нуля компонент по прежним k осям. Можно показать, что эти два взаимоисключающих подпространства ортогональны относительно друг друга.

Точки k и (n–k)-мерных подпространств полностью определяют все точки n-мерного пространства сети.

3. Наконец, если сеть из n катушек рассматривается как ортогональная сеть, имеющая как контурные, так и узловые токи, то точка описывает траекторию в n-мерном пространстве сети и имеет проекции на все n координатных осей.

Можно считать, что сеть из n катушек представляет гипотетическое n-мерное пространство независимо от числа контуров и узловых пар в сети. В зависимости от способа соединения катушек n-мерное пространство разделяется на два независимых ортогональных подпространства с взаимоисключающими друг друга точками, так что движущаяся точка может ограничивать свое движение одним из двух подпространств в зависимости от способа возбуждения сети. Следовательно, токи, протекающие в контурах, и токи, протекающие через узловые пары, ортогональны друг другу.

11. ОГРАНИЧЕННОСТЬ ДАННОГО ГЕОМЕТРИЧЕСКОГО ПРЕДСТАВЛЕНИЯ

I. В геометрической интерпретации электрических явлений, возникающих в сетях, представляющее пространство, в котором движется точка, не подразумевает существования каких-либо границ. В начале координат этого пространства можно допустить существование бесконечного числа координат систем, некоторые из которых соответствуют:

1) определенной n-катушечной сети, выделенной из всех возможных n-катушечных сетей;
2) определенному множеству n осей, принятому в этой n-катушечной сети;
3) определенной линейной функции от n токов, протекающих в предполагаемых n осях данной сети (скажем, “намагничивания” или “нагрузки”, соответствующих n выбранным частным токам).

II. Однако представление об n-мерном пространстве, простирающемся во всех направлениях до бесконечности, допускающем бесконечное разнообразие координатных систем, связанных произвольным выбором линейного преобразования, не соответствует представлению об n-катушечной сети, поскольку для n-катушечной сети не все линейные преобразования возможны. Существует ограниченное (хотя и большое) число способов соединения n катушек. Существует ограниченное число способов, которыми могут быть выбраны n осей, и ограниченное число способов, которыми произвольные линейные отношения (гипотетические токи) могут заменять действительные выбранные токи.

Другими словами, в представленном n-мерном пространстве все возможные значения токов, которые возможны в любой n-катушечной сети, всегда могут быть полностью показаны, но не наоборот. В выбранном пространстве точка может следовать по траекториям, которые нельзя воспроизвести действительными или гипотетическими токами любой n-катушечной сети, а следовательно, принятое пространство неточно воспроизводит все возможные сети. Не существует взаимооднозначного соответствия между введенным пространством и сетью, которое необходимо для дальнейшего использования геометрического представления. Например, в представляющем пространстве нет ничего, что оправдывало бы существование двойственных понятий “контур” и “узловая пара”, которые играют основную роль в анализе сетей.

III. Чтобы найти геометрическое представление, в котором физические понятия “контур”, “узловая пара” и другие находят точный геометрический эквивалент, характер представляющего пространства, рассматриваемого до сих пор, следует ограничить введением границ, удалением частей, добавлением областей проектирования, пока представляющее пространство не приобретет ту же форму, что и сама сеть.

IV. Исследование n-мерных пространств, не ограниченных во всех направлениях, является областью “дифференциальной геометрии”; исследование n-мерных пространств, ограниченных в разных направлениях пространствами меньшей размерности (таких, как куб или икосаэдр), является областью “топологии” (“Analysis Situs”) ¹⁾, где такие ограниченные пространства известны как “ячейки”, разных размерностей.

Тензорная методология (т. е. использование “систем координат”, “преобразований”, “инварианта” и “группы”) используется в исследованиях по дифференциальной геометрии уже более 50 лет, на эту тему имеется обширная литература; исследование в топологии с систематическим использованием тензорной символики начали использовать год-два назад, но до сих пор литературы по этому вопросу нет, если не считать нескольких рефератов и обсуждений.

I. Катушка может быть геометрически представлена одномерным пространством (линией), которое ограничено двумя точками, двумя узлами катушки. Узловая точка двух катушек также может быть представлена как нульмерное пространство.

Следовательно, сеть из n катушек и k узлов можно представить геометрически как совокупность n одномерных пространств и k нульмерных пространств, где нульмерные пространства образуют границы одномерных пространств. С геометрической точки зрения безымпедансная ветвь должна считаться катушкой с нулевым импедансом. (Следовательно, ее нужно представлять одномерным пространством (1-ячейкой), а два ее конца – нульмерными пространствами (0-ячейки), что совершенно не соответствует тому, что мы излагали выше. В нашем списании безымпедансная ветвь образует один узел).

Когда вращающиеся машины со щетками и контактными кольцами связываются в сеть, но полная система еще остается невозбужденной, представляющее пространство, в добавление к нуль- и одномерным пространствам, пополняется двухмерными и вообще k-мерными пространствами.

II. Классификация и изучение свойств этих сложных геометрических фигур и установление их общих свойств слишком сложны, в помощь им требуется дополнительный геометрический аппарат. Он состоит в наложении на такие совокупности пространств геометрических конфигураций различной размерности. Способ, с помощью которого эти дополнительные сетки можно изображать на данных ячейках, служит исходной точкой для их дальнейшего изучения и классификации. Эти дополнительные геометрические конфигурации, накладываемые на данные “ячейки” для изучения их свойств, называются “цепями”.

_______________
¹⁾ А именно алгебраической (комбинаторной) топологии в отличие от теоретико-множественной топологии, изучающей непрерывные свойства геометрических систем, дифференциальное и интегральное исчисление, теорию функций и т.д. (Прим. пер.).

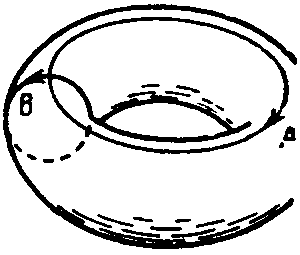
Например, тор (или “бублик”, рис. 8.7.) отличается от сферы тем, что на нем можно изобразить две (и только две) замкнутые кривые: одна параллельна отверстию (А); другая перпендикулярна отверстию (В). Характерным для этих замкнутых кривых является то, что они не могут исчезнуть с поверхности тора при деформациях, растяжениях, изгибании и перемещении (без удаления их с поверхности тора). С другой стороны, любая замкнутая кривая на сфере исчезает при стягивании сферы в точку.

Рис. 8.7. Top, или “бублик”, с двумя инвариантными замкнутыми кривыми.

Таким образом, различие между сферой и тором устанавливается с помощью конфигураций (“цепей”), накладываемых на ниx. Из-за наличия этих двух инвариантных замкнутых кривых тор называется “поверхностью 1-го рода”, в то время как сфера из-за их отсутствия называется “поверхностью 0-го рода”.

III. Заметим теперь, что наложение “цепей” на “ячейки” совершенно аналогично наложению “электромагнитных величин” (токов, напряжений, потоков, МДС и т. п.) на “сеть”. Изучать сети для инженерных приложений можно только наложением электромагнитных величин.

Этот процесс классификации сетей или ячеек с помощью накладываемых цепей или электромагнитных величин аналогичен изучению задач статики как частного случая задач динамики.

Процесс наложения цепей на ячейки и электромагнитных величин на сети является плодотворным аналитическим “инструментом”, так как этот процесс наложения цепей или электромагнитных величин позволяет обнаружить “группу” (см. гл. 11).

13. АНАЛОГИ СЕТЕВЫХ ПОНЯТИЙ В ТОПОЛОГИИ

I. Топологические эквиваленты некоторых сетевых понятий, основанные на номенклатуре Веблена, даны в следующей таблице:

Сеть	Одномерный комплекс
Подсеть	Подкомплекс
Катушка	1-ячейка
Узел	0-ячейка
Контур	1-цепь
Узловая пара	Ограничивающая 0-цепь

Сеть также известна как “линейный граф” топологии Веблена. Когда указано направление для выражений левой части, то прилагательное “ориентированный” добавляется к выражениям правой части таблицы, например, “ориентированная 1-цепь”.

Другими соответствующими понятиями являются:

Чисто узловая сеть	Дерево
Число контуров	Цикломатическое число

II. Наложение электромагнитных величин на сеть топологически эквивалентно наложению “цепей” на “ячейки”. Некоторые аналоги сетевых понятий в топологии даны в номенклатуре Такера в следующей таблице:

Контурный ток iα	1-цепь
Ток, входящий в узел	Граница 1-цепи
Абсолютный потенциал узла	Двойственная 0-цепь
Напряжение на катушке eα	Граница двойственной 0-цепи
Мощность eαiα	Индекс пересечения

Топологическая номенклатура в тензорном способе описания до сих пор еще не установлена.

14. ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВ-СТРУКТУР

I. Различные типы преобразований i = Сi΄, используемые в книге, можно из физических соображений грубо разбить на два типа преобразований:

1) действительных токов в действительные токи;
2) действительных токов в гипотетические токи.

II. Первые преобразования, использующие только действительные физически существующие токи, можно еще раз разделить на два типа: 1) превращение токов, протекающих в одной системе ветвей, в токи, протекающие в другой системе ветвей при сохранении самой сети; 2) изменение токов при переходе от одного способа соединения ветвей к другому, т. е. при изменении самой сети.

Первый тип преобразования можно рассматривать как обычное “преобразование координат”. Однако второй тип преобразования включает в себя новое содержание, поскольку разрушаются соединения катушек и одна сеть заменяется другой.

III. С геометрической точки зрения второй тип понятия “преобразование” С^α_α΄, используемый в этой книге для изменения взаимосоединений в сетях, может быть выражен в следующей форме.

Дано множество из n пространств-компонент, взаимосвязанных различным образом и образующих, следовательно, огромное число новых пространств (или пространств-структур). Каждое из этих пространств-структур имеет свое множество координатных систем. Если на каждое из них наложена некоторая геометрическая конфигурация (скажем, множество траекторий или “путей”), то можно установить систему уравнений (типа e = z х i) для каждого пространства-структуры, в котором расположена эта конфигурация.

Рассматриваемая проблема состоит в установлении группы матриц преобразования С^α_α΄, которые преобразуют эти уравнения конфигураций, различные в разных пространствах-структуpax, одно в другое. Другими словами, проблема состоит в нахождении уравнения e΄ = z΄ х i΄ некоторой конфигурации, если уравнение конфигурации e = z х i известно для одного пространства-структуры. Или, короче, проблема состоит в установлении соответствия между конфигурациями, которые наложены на различные пространства-структуры.

IV. С физической точки зрения эту же проблему можно сформулировать следующим образом.

Дано множество различных сетей, каждая из которых имеет различное число подсетей, контуров и узловых пар (но то же число тех же самых катушек). Если к ним приложены токи и напряжения, то поведение каждой сети описывается системой уравнений (скажем, e = z х i). Проблема состоит в установлении группы преобразований С^α_α΄, с помощью которой можно найти уравнение каждой сети, если для одной сети оно уже установлено.

Система уравнений i^α = С^α_α΄i^α΄ изменяет не только систему координат α на α΄, но и пространство-структуру, в котором располагаются системы координат, поскольку α и α΄ лежат в двух различных пространствах-структурах. Или уравнение i^α = С^α_α΄i^α΄ преобразует часть одного пространства-структуры в часть другого пространства-структуры (а именно те точки, которые лежат на конфигурации).

V. Подводя итоги, отметим, что одной из задач инженера является установление и численный анализ уравнений движения разнообразных динамических систем в различных условиях. Обычный метод атаки состоит в анализе каждой возникающей задачи и в установлении уравнений движения из фундаментальных физических принципов. В этом случае можно изменять оси одной и той же системы, но нельзя заменять саму систему другой, так как обычный метод анализа не дает возможности переходить из одного пространства-структуры в другое с другим множеством координатных систем.

Основная цель книги и состоит в предложении новой процедуры, которая включает одновременный анализ разнообразия физически подобных, но тем не менее различных систем. Здесь предлагается делать первый шаг при анализе лю6ой физической системы в направлении установления матрицы преобразования С^α_α΄, которая определяет “соответствие” между уравнением движения исследуемой системы и уравнением движения другой системы (примитивной), которое уже известно. Как только С^α_α΄ установлена, оставшаяся работа состоит из рутинных вычислений. После того как найдена “группа” С^α_α΄, анализ большого разнообразия физических систем становится рутинной процедурой.

VI. Следует напомнить, что в большинстве инженерных задач понятие “преобразование” i^α = С^α_α΄ х i^α΄ включает “преобразование путей из одного пространства-структуры в другое”, а не просто “преобразование системы координат” в том же пространстве.

Соответствие между различными типами сетей (пространств-структур) устанавливается признанием того, что для всех чисто контурных сетей существует одна и только одна система координат, в которой уравнения движения различных сетей идентичны. Эта система координат состоит из отдельных катушек сети.

Таким образом, если в двух n-катушечных, n-контурных сетях (имеющих различное число подсетей) заданы n переменных в n катушках, то n уравнений движения идентичны. Они не будут идентичными, если в одной из сетей выбрано другое множество ветвей.

VII. В главе о синтезе будет показано, что можно установить преобразование между “путями”, наложенными на пространства-структуры, в которых каждая структура содержит различное число и разные типы составляющих пространств при условии, что на пути наложено определенное ограничение (скажем, все сети питаются постоянным током).